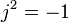Admisión
En Ingeniería eléctrica, admisión es una medida de cuán fácilmente un circuito o dispositivo permitirá una corriente fluyendo. Se define como el inversa de impedancia. El SI unidad de admisión es la Siemens (símbolo S). Oliver Heaviside acuñó el término admisión en diciembre de 1887.[1]
Admisión se define como
donde
- Y es la admitancia, medida en Siemens
- Z es la impedancia, medida en ohmios
La unidad sinónima MHO, y el símbolo ℧ (un revés en mayúscula omega Ω), son también de uso común.
Resistencia es una medida de la oposición de un circuito al flujo de una corriente constante, mientras que la impedancia toma en cuenta no sólo la resistencia sino también los efectos dinámicos (conocidos como reactancia). Asimismo, admisión no es sólo una medida de la facilidad con la cual puede fluir una corriente constante, sino también los efectos dinámicos de susceptancia del material a la polarización:
donde
 es la entrada, medida en siemens.
es la entrada, medida en siemens. es el conductancia, medida en siemens.
es el conductancia, medida en siemens. es el susceptancia, medida en siemens.
es el susceptancia, medida en siemens.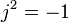
Conversión de impedancia de entrada
- Partes de este artículo o sección se basan en el conocimiento del lector del complejo impedancia representación de condensadores y inductores y en el conocimiento de la dominio de la frecuencia representación de señales.
La impedancia, Z, se compone de partes reales e imaginarias,
donde
- R es la resistencia, medida en ohmios
- X es la reactancia, medida en ohmios
Entrada, al igual que la impedancia, es un número complejo, formado por un real parte (la conductancia, G) y un imaginario parte (la susceptancia, B), así:
donde G (conductancia) y B (susceptancia) está dada por:
La magnitud y la fase de la admitancia están dada por:
donde
- G es la conductancia, medida en Siemens
- B es la susceptancia, también medido en Siemens
Tenga en cuenta que (como se muestra arriba) los signos de reactancias invertidos en el dominio de admisión; es decir, susceptancia capacitiva es positiva y susceptancia inductivo es negativo.
Véase también
| Mire para arriba admisión en Wiktionary, el diccionario libre. |
- Matriz de admitancia nodal
- Unidades del electromagnetismo
- Immittance
Referencias
- ^ Ushida, Jun; Tokushima, Masatoshi; Shirane, Masayuki; Gomyo, Akiko; Yamada, Hirohito (2003). "Immittance que empareja para cristales fotónicos de sistemas abiertos multidimensionales". Physical Review B 68 (15). arXiv:Cond-mat/0306260. Bibcode:2003PhRvB...68o5115U. Doi:10.1103/PhysRevB.68.155115.

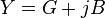
 es la entrada, medida en siemens.
es la entrada, medida en siemens. es el conductancia, medida en siemens.
es el conductancia, medida en siemens. es el susceptancia, medida en siemens.
es el susceptancia, medida en siemens.