Déficit esperado

Déficit esperado (ES) es un medida del riesgo, un concepto que se utiliza en las finanzas (y más concretamente en el campo de la medición del riesgo financiero) para evaluar la riesgo de mercado o riesgo de crédito de una cartera. Es una alternativa a valor en riesgo es más sensible a la forma de la distribución de pérdida en la cola de la distribución. El "déficit esperado nivel q %" es la rentabilidad esperada de la cartera en el peor $q$ % de los casos.

También se llama déficit esperado valor condicional en riesgo (CVaR), promedio del valor en riesgo (AVaR), y pérdida esperada cola (ETL).

ES evalúa el valor (o riesgo) de una inversión de una manera conservadora, centrándose en los resultados menos rentables. Para valores altos de $q$ ignora las posibilidades más rentables pero improbables, para valores pequeños de $q$ se centra en las peores pérdidas. Por otro lado, a diferencia del pérdida máxima con descuento incluso para valores menores de $q$ déficit esperado no tiene en cuenta sólo los resultados más catastróficos único. Un valor de $q$ de uso frecuente en la práctica es del 5%.^{[citación necesitada]}

Prevé déficit es un coherentey además un espectral, medida de riesgo de la cartera financiera. Se requiere un cuantil-nivel $q$ y se define como la pérdida esperada de cartera valor dado que una pérdida ocurre en o por debajo de la $q$ -quantile.

Contenido

1 Definición formal
2 Ejemplos
3 Propiedades
4 Déficit esperado dinámico
5 Véase también
6 Referencias

Definición formal

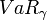If $X \in L^p(\mathcal{F})$ (un Espacio LP) es la recompensa de una cartera en algún tiempo futuro y $0 < \alpha < 1$ luego definimos el déficit esperado como $ES_{\alpha} = \frac{1}{\alpha}\int_0^{\alpha} VaR_{\gamma}(X)d\gamma$ donde $VaR_{\gamma}$ es el Valor en riesgo. 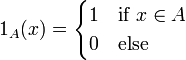Esto puede ser equivalente escrito como $ES_{\alpha} = -\frac{1}{\alpha}\left(E[X \ 1_{\{X \leq x_{\alpha}\}}] + x_{\alpha}(\alpha - P[X \leq x_{\alpha}])\right)$ donde $x_{\alpha} = \inf\{x \in \mathbb{R}: P(X \leq x) \geq \alpha\}$ es el menor $\alpha$ -cuantil y $1_A(x) = \begin{cases}1 &\text{if }x \in A\\ 0 &\text{else}\end{cases}$ es el función del indicador.^[1] Es la representación dual

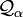ES_{\alpha} = \inf_{Q \in \mathcal{Q}_{\alpha}} E^Q[X]

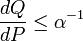donde $\mathcal{Q}_{\alpha}$ es el conjunto de medidas de probabilidad ¿Cuáles son absolutamente continua a la medida física $P$ tal que $\frac{dQ}{dP} \leq \alpha^{-1}$ casi con toda seguridad.^[2] Tenga en cuenta que $\frac{dQ}{dP}$ es el Derivado de Radon-Nikodym de $Q$ con respecto a $P$ .

Si la distribución subyacente para $X$ es una distribución continua entonces el déficit previsto es equivalente a la expectativa condicional cola definido por $TCE_{\alpha}(X) = E[-X\mid X \leq -VaR_{\alpha}(X)]$ .^[3]

Informalmente, y no con rigor, esta ecuación equivale a decir "en caso de pérdidas tan graves que ocurren sólo alfa por ciento del tiempo, lo que es nuestra pérdida promedio".

Déficit esperado también puede escribirse como una medida del riesgo de distorsión otorgado por la función de distorsión $g(x) = \begin{cases}\frac{x}{1-\alpha} & \text{if }0 \leq x < 1-\alpha,\\ 1 & \text{if }1-\alpha \leq x \leq 1.\end{cases}$ ^[4]^[5]

Ejemplos

Ejemplo 1. Si creemos que nuestra pérdida media en el peor 5% de los resultados posibles para nuestra cartera es 1000 euros, entonces podríamos decir que nuestro déficit esperado es 1000 euros para la cola de 5%.

Ejemplo 2. Considere una cartera que tendrá los siguientes valores posibles al final del período:

probabilidad	valor final
del evento	de la cartera
10%	0
30%	80
40%	100
20%	150

Ahora Supongamos que pagamos 100 al principio del período de esta cartera. Entonces el beneficio en cada caso)valor final−100) o:

probabilidad
del evento	beneficio
10%	−100
10g	−20
40%	0
20%	50

En esta tabla nos calcular el déficit esperado $ES_q$ para unos valores de $q$ :

$q$	déficit esperado $ES_q$
5%	−100
10%	−100
20%	−60
30%	−46.6
40%	−40
50%	−32
60%	−26.6
80%	−20
90%	−12.2
100%	−6

Para ver cómo estos valores fueron calculados, considerar el cálculo de $ES_{0.05}$ , la expectativa en el peor 5% de los casos. Estos casos pertenecen a (son un subconjunto de) fila 1 de la tabla de ganancias, que tienen un beneficio de −100 (pérdida total de los 100 invertido). El beneficio esperado para estos casos es −100.

Ahora consideremos el cálculo de $ES_{0.20}$ , la expectativa en el peor de los casos 20 de cada 100. Estos casos son los siguientes: 10 casos de fila uno y 10 casos de fila dos (tenga en cuenta que 10 + 10 es igual a los deseada 20 casos). Para la fila 1 existe un beneficio de −100, mientras que para la fila 2 a beneficio de −20. Conseguimos mediante la fórmula de valor esperado

\frac{ \frac{10}{100}(-100)+\frac{10}{100}(-20) }{ \frac{20}{100}} = -60.

Del mismo modo para cualquier valor de $q$ . Seleccionamos tantas filas a partir de la parte superior que sean necesarios para dar una probabilidad acumulativa de $q$ y luego calcular una expectativa sobre esos casos. En general la última fila seleccionada no puede totalmente utilizarse (por ejemplo en el cálculo $ES_{0.20}$ Utilizamos solamente 10 de los 30 casos por cada 100 proporcionados por la fila 2).

Como un último ejemplo, calcular $ES_1$ . Es la expectativa en todos los casos, o

0.1(-100)+0.3(-20)+0.4\cdot 0+0.2\cdot 50 = -6. \,

El Valor en riesgo (Var) se da por debajo para la comparación.

$q$	$\operatorname{VaR}_q$
0% ≤ $q$ < 10%	−100
≤ 10% $q$ < 40%	−20
≤ 40% $q$ < 80%	0
≤ 80% $q$ ≤ 100%	50

Propiedades

El déficit previsto $ES_q$ aumenta a medida que $q$ aumenta.

El déficit previsto de 100%-quantile $ES_{1.0}$ equivale a la valor esperado de la cartera.

Para una cartera determinada, el déficit esperado $ES_q$ es mayor o igual al valor en riesgo $\operatorname{VaR}_q$ en la misma $q$ nivel.