Duración del bono
| Mercados financieros |
|---|
 |
|
| Mercado de bonos |
|
| Mercado de valores |
|
| Otros mercados |
|
Derivados
Cambio de divisas
|
| Medicamentos de venta libre (off-exchange) |
|
| Comercio |
|
| Áreas relacionadas con la |
|
En Finanzas, la duración de una financiera activo consta de fijo flujos de efectivo, por ejemplo un bonos, es la promedio ponderado de los tiempos hasta los flujos de caja fijadas se reciben. Cuando un activo se considera como una función de rendimiento, duración también mide la sensibilidad del precio a la producción, la tasa de cambio de precio con respecto a la producción o el cambio porcentual en el precio de un cambio paralelo en los rendimientos.[1][2][3]
El doble uso de la palabra "duración", como ambos el tiempo promedio ponderado hasta el pago y como el cambio porcentual en el precio, a menudo causa confusión. Estrictamente hablando, Duración de Macaulay es el nombre dado al tiempo promedio ponderado hasta que los flujos de efectivo se reciben y se mide en años. Duración modificada es el nombre dado a la sensibilidad al precio y el cambio porcentual en el precio para una unidad de cambio en el rendimiento.
Ambas medidas se llaman "duración" y tienen el mismo (o cerca de la misma) valor numérico, pero es importante tener en cuenta las distinciones conceptuales entre ellos.[4] Duración de Macaulay es una medida de tiempo con unidades en años y realmente tiene sentido sólo para un instrumento con flujos fijos. Para un enlace estándar la duración de Macaulay será entre 0 y la madurez del bono. Es igual a la madurez si y sólo si el vínculo es un bonos cupón cero.
Duración modificada, por el contrario, es un derivado (tasa de cambio) o sensibilidad al precio y medidas del porcentaje de cambio de precio con respecto a la producción. (Sensibilidad al precio con respecto a los rendimientos también se puede medir en términos absolutos (dólar), y la sensibilidad absoluta se refiere a menudo como duración de dólarRiesgo DV01, BPV o delta (δ o Δ)). El concepto de duración modificada se puede aplicar a instrumentos sensibles a tasas de interés con flujos de efectivo no fija y por lo tanto puede ser aplicado a una amplia gama de instrumentos que duración de Macaulay. Duración modificada se utiliza más a menudo que la duración de Macaulay.
Para el uso de cada día, la igualdad o cerca de la igualdad de los valores de Macaulay y la duración modificada puede ser una ayuda útil a la intuición. Por ejemplo un bono de cupón estándar de diez años tendrá duración de Macaulay algo pero no considerablemente menos de 10 años y de esto podemos inferir que la duración modificada (sensibilidad al precio) también será algo pero no dramáticamente inferior al 10%. Del mismo modo, un bono de cupón de dos años tendrá duración Macaulay algo por debajo de 2 años y la duración modificada un poco por debajo del 2%. (Por ejemplo un bono de nominal de 5% de diez años tiene una duración modificada de 7.8% mientras que un bono de nominal de 5% de dos años tiene una duración modificada del 1,9%).
Contenido
- 1 Duración de Macaulay
- 2 Duración modificada
- 2.1 Periódicamente se agrava
- 2.2 Unidades
- 2.3 Flujos de efectivo no-fijo
- 2.4 Cambios de producción finita
- 3 Duración de Fisher – Weil
- 4 Duración de la tasa clave
- 5 Fórmulas de duración del vínculo
- 5.1 Ejemplo
- 6 Duración de dólares, Bloomberg DV01, BPV, «Riesgo»
- 6.1 Aplicación al valor en riesgo (VaR)
- 7 Riesgo - duración como sensibilidad de la tasa de interés
- 8 Opciones de encajado y duración efectiva
- 9 Duración de la propagación
- 10 Duración media
- 11 Convexidad
- 12 Véase también
- 13 Notas
- 14 Referencias
- 15 Lectura adicional
- 16 Acoplamientos externos
Duración de Macaulay
Duración de Macaulay, llamado así por Frederick Macaulay que introdujo el concepto, es la promedio ponderado madurez de flujos de efectivo. Considere un conjunto fijados de flujos de efectivo. El valor actual Estos flujos de efectivo es:
La duración de Macaulay se define como:[1][2][3][5]
-
(1)

donde:
 índices de los flujos de efectivo,
índices de los flujos de efectivo,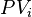 es el valor actual de la
es el valor actual de la  pago en efectivo de TH de un activo,
pago en efectivo de TH de un activo, es el tiempo en años, hasta el
es el tiempo en años, hasta el  recibirán pago de TH,
recibirán pago de TH, es el valor presente de los pagos de efectivo futuros del activo.
es el valor presente de los pagos de efectivo futuros del activo.
En la segunda expresión el término fraccionario es el cociente entre el flujo de efectivo 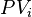 al PV total. Estos términos a 1.0 y servir como pesos para un promedio ponderado. Por lo tanto la expresión general es un promedio ponderado de tiempo hasta los pagos de flujo de caja, con peso
al PV total. Estos términos a 1.0 y servir como pesos para un promedio ponderado. Por lo tanto la expresión general es un promedio ponderado de tiempo hasta los pagos de flujo de caja, con peso  siendo la proporción del valor actual del activo debido al flujo de efectivo
siendo la proporción del valor actual del activo debido al flujo de efectivo  .
.
Para un conjunto de flujos de efectivo fijados positivo todo caerá la media ponderada entre 0 (el tiempo mínimo), o más precisamente 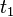 (el tiempo al primer pago) y el tiempo de flujo de caja final. La duración de Macaulay será igual a la madurez final si y sólo si hay sólo un único pago al vencimiento. En símbolos, si los flujos de efectivo son, en orden,
(el tiempo al primer pago) y el tiempo de flujo de caja final. La duración de Macaulay será igual a la madurez final si y sólo si hay sólo un único pago al vencimiento. En símbolos, si los flujos de efectivo son, en orden,  , entonces:
, entonces:
las desigualdades siendo estricta a menos que tenga un único flujo de efectivo. En cuanto a bonos estándar (para que flujos de efectivo son fijos y positivo), esto significa que la duración de Macaulay será igual a la madurez del bono sólo para un bono de cupón cero.
Duración de Macaulay tiene la interpretación esquemática que se muestra en la figura 1.

Esto representa el vínculo en el siguiente ejemplo: dos años vencimiento con un cupón de 20% y continuamente compuesto rendimiento de 3.9605%. Los círculos representan el valor presente de los pagos, con los pagos de cupón cada vez más pequeñas cuanto más en el futuro son y el pago final grandes incluyendo el pago de cupón y el reembolso final del principal. Si estos círculos fueron puestos en una viga de equilibrio, el fulcro (centro de equilibrio) de la viga representaría la distancia promedio ponderada (tiempo de pago), que es en este caso años 1,78.
Para cálculos más prácticos, la duración de Macaulay se calcula utilizando la rendimiento al vencimiento para calcular el  :
:
-
(2)

-
(3)

Donde:
 índices de los flujos de efectivo,
índices de los flujos de efectivo,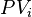 es el valor actual de la
es el valor actual de la  pago en efectivo de un activo, TH
pago en efectivo de un activo, TH es el flujo de efectivo de la
es el flujo de efectivo de la  pago del TH de un activo,
pago del TH de un activo, es el rendimiento al vencimiento (continuamente compuesta) para un activo,
es el rendimiento al vencimiento (continuamente compuesta) para un activo, es el tiempo en años, hasta el
es el tiempo en años, hasta el  recibirán pago de TH,
recibirán pago de TH, es el valor presente de los pagos de efectivo del activo hasta su vencimiento.
es el valor presente de los pagos de efectivo del activo hasta su vencimiento.
Macaulay dio dos medidas alternativas:
- Expresión (1) Duración de Fisher – Weil que los precios de los bonos cupón cero de utiliza como factores de descuento, y
- Expresión (3) rendimiento de los bonos al vencimiento se utiliza para calcular los factores de descuento.
La diferencia clave entre las duraciones de dos es que la duración de Fisher – Weil permite la posibilidad de una curva de pendiente, mientras que la segunda forma se basa en un valor constante de la producción  , no variando por plazo de pago. Con el uso de computadoras, ambas formas se pueden calcular pero expresión (3), suponiendo un rendimiento constante, es más ampliamente utilizado debido a la aplicación a la duración modificada.
, no variando por plazo de pago. Con el uso de computadoras, ambas formas se pueden calcular pero expresión (3), suponiendo un rendimiento constante, es más ampliamente utilizado debido a la aplicación a la duración modificada.
Duración y vida media ponderada
Similitudes en los valores y definiciones de la duración de Macaulay versus vida media ponderada pueden llevar a confundir el objetivo y el cálculo de los dos. Por ejemplo, 5 años tasa fija de interés de bonos sólo tendría una vida media ponderada de 5 y una duración de Macaulay que debe estar muy cerca. Las hipotecas se comportan semejantemente. Las diferencias entre ambos son las siguientes:
- Duración Macaulay sólo mide flujos de período fijados, factores de vida promedio ponderado en todos los principales flujos de efectivo ya sea fijo o flotante. Así para las hipotecas de brazo de híbrido de período fijo, para el modelado de efectos, todo el fijo período termina en la fecha de efectuar el último pago fijo o el mes anterior para reiniciar.
- Duración de Macaulay descuenta todos los flujos de efectivo en el correspondiente costo de capital. Vida media ponderada no descuento.
- Duración de Macaulay utiliza principal y el interés cuando los flujos de efectivo de la carga. Vida media ponderada sólo utiliza a principal.
Duración modificada
En contraste con la duración de Macaulay, duración modificada (a veces abreviado MD) es una medida de sensibilidad de precio, definida como el porcentaje derivado del precio con respecto a la producción. Duración modificada se aplica cuando un enlace u otro activo se considera como una función de producción. En este caso se puede medir el derivado logarítmico con respecto al rendimiento:
Así para los enlaces de pago fijo, cuando se expresa el rendimiento continuamente compuesto, duración de Macaulay y la duración modificada son iguales.
En primer lugar, consideremos el caso de los rendimientos compuestos continuamente. Si tomamos la derivada del precio o valor presente, la expresión (2), en relación con el rendimiento continuamente compuesto  vemos que:
vemos que:
En otras palabras, para los rendimientos expresado continuamente compuesto,
-
 .
[1]
.
[1]
donde:
 índices de los flujos de efectivo,
índices de los flujos de efectivo, es el tiempo en años, hasta el
es el tiempo en años, hasta el  recibirán pago de TH,
recibirán pago de TH, es el valor presente de los pagos de efectivo del activo.
es el valor presente de los pagos de efectivo del activo.
Periódicamente se agrava
En los mercados financieros, los rendimientos se expresan periódicamente compuesto (decir anual o semestral) en vez de compuesto continuamente. Entonces se convierte en expresión (2):
Para encontrar la duración modificada, cuando tomamos la derivada del valor  con respecto a la producción periódicamente compuesta encontramos [6]
con respecto a la producción periódicamente compuesta encontramos [6]
Reorganizar (dividiendo ambos lados por -V) da:
que es la bien conocida relación entre la duración modificada y la duración de Macaulay:
donde:
 índices de los flujos de efectivo,
índices de los flujos de efectivo, es la frecuencia de composición por año (1 para anual, 2 para el semestral, 12 meses, 52 para el semanal, etc.),
es la frecuencia de composición por año (1 para anual, 2 para el semestral, 12 meses, 52 para el semanal, etc.), es el flujo de efectivo de la
es el flujo de efectivo de la  pago del TH de un activo,
pago del TH de un activo, es el momento en años hasta que el
es el momento en años hasta que el  recibirán pago de TH (por ejemplo, una semestral dos años estaría representada por un
recibirán pago de TH (por ejemplo, una semestral dos años estaría representada por un  Índice de 0.5, 1.0, 1.5 y 2.0),
Índice de 0.5, 1.0, 1.5 y 2.0),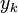 es el rendimiento al vencimiento de un activo, agravado periódicamente
es el rendimiento al vencimiento de un activo, agravado periódicamente es el valor presente de los pagos de efectivo del activo.
es el valor presente de los pagos de efectivo del activo.
Esto le da a la bien conocida relación entre duración de Macaulay y la duración modificada citado anteriormente. Se debe recordar que, aunque la duración de Macaulay y duración modificada están estrechamente relacionados, son conceptualmente distintos. Duración de Macaulay es un tiempo promedio ponderado hasta el reembolso (medido en unidades de tiempo tal como años) mientras que la duración modificada es una medida de sensibilidad del precio cuando el precio se trata como una función de producción, la porcentaje de cambio en precio con respecto a la producción.
Unidades
Duración modificada las unidades comunes son el cambio porcentual en el precio por un porcentaje punto de cambio en rendimiento al año (rendimiento ejemplo pasando de 8% por año (y = 0.08) 9% por año (y = 0. 09)). Esto le dará duración modificada cerca del valor de Macaulay duración (y lo mismo cuando las tasas se agravan continuamente).
Formalmente, la duración modificada es un semi-elasticidad, la por ciento cambio en el precio para un unidad cambio en el rendimiento, en lugar de un elasticidad, que es un cambio de porcentaje en la salida de un porcentaje cambio en la entrada. Duración modificada es una tasa de cambio, el cambio porcentual en el precio por cambio en el rendimiento.
En derivados de precios ("Los griegos"), la cantidad análoga más cercano es Rho, que es la elasticidad de precio (cambio porcentual en el precio de porcentaje cambio en tasa de interés), y, a diferencia de la duración modificada, es una real elasticidad.
Flujos de efectivo no-fijo
Duración modificada puede ampliarse a instrumentos con flujos de efectivo no-fijos, mientras que la duración de Macaulay se aplica sólo a los instrumentos de flujo de efectivo fijo. Duración modificada se define como la derivada logarítmica del precio con respecto a rendimiento y tal definición se aplica a instrumentos que dependen de los rendimientos, o no se fijan los flujos de efectivo.
Cambios de producción finita
Duración modificada se define por encima como un derivado (como el término se refiere al cálculo) y se basa en cambios infinitesimales. Duración modificada es también útil como una medida de la sensibilidad del precio de mercado de un bono a finito tasa de interés (es decir, rendimiento) movimientos. Para un pequeño cambio en el rendimiento, 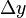 ,
,
Así la duración modificada es aproximadamente igual al cambio porcentual en el precio para un cambio finito dado de rendimiento. Así que un bono de 15 años con una duración de Macaulay de 7 años tendría una duración modificada de aproximadamente 7 años y caería aproximadamente un 7% en valor si la tasa de interés aumenta en un punto porcentual (digamos de 7% al 8%).[7]
Duración de Fisher – Weil
Duración de Fisher – Weil es un refinamiento de la duración de Macaulay que toma en cuenta la estructura de plazos de tasas de interés. Duración de Fisher – Weil calcula que el valor actual de los flujos de caja relevantes (más estricta) mediante el uso del cupón cero rendimiento para cada vencimiento respectivo.[8]
Duración de la tasa clave
Duración de la tasa clave (también llamado DV01s parcial o duraciones parciales) es una extensión natural de la duración modificada total para medir sensibilidad a los cambios de diferentes partes de la curva de rendimiento. Clave tipo de duraciones podrían definirse, por ejemplo, con respecto al cupón cero tarifas con madurez '1 M', '3 M', M ' 6', '1Y', '2Y', '3', '5Y', '7Y', '10Y', '15', '20Y', '25Y', '30Y'. Ho (1992) [9] introdujo el término tasa clave duración. Reitano cubre modelos de curva de rendimiento multifactorial desde 1991 [10] y ha revisado el tema en una revisión reciente.[11]
Duración de la tasa clave requiere que un instrumento de una curva de rendimiento de valor y requiere de la construcción de una curva de rendimiento. Metodología original de Ho se basa en la valoración de instrumentos de un cero o curva de rendimiento de punto y utiliza la interpolación lineal entre"claves", pero la idea es aplicable a curvas basadas en tasas de avance, las tasas de par y así sucesivamente. Muchos problemas técnicos ocurren durante períodos de tasa clave (DV01s parcial) que no se presentan por la duración modificada total estándar debido a la dependencia de la duración de la tasa clave en el tipo específico de la curva de rendimiento utilizado para valorar los instrumentos (véase Coleman, 2011 [3]).
Fórmulas de duración del vínculo
Para un enlace estándar con pagos fijos, semestral el formula de forma cerrada de duración en enlace es:[citación necesitada]
- FV = valor nominal
- C = pago de cupón por período (semestre)
- i = tasa de descuento por período (semestre)
- a = fracción de un período restante hasta el próximo pago de cupón
- m = número de períodos hasta el vencimiento de cupón completo
- P = precio del bono (valor actual de flujos de efectivo descontados con la tasa de i)
Un bono con frecuencia cupón  pero un número entero de períodos (por lo que no existe ningún período de pago fraccionado), la fórmula se simplifica a: [12]
pero un número entero de períodos (por lo que no existe ningún período de pago fraccionado), la fórmula se simplifica a: [12]
donde
- y = Rendimiento (por año, en forma decimal),
- c = Cupón (por año, en por ciento),
- m = Número de períodos de la cupón.
Ejemplo
Considere un bono de 2 años con valor nominal de $100, un cupón semestral de 20% y un rendimiento de 4% compuesto semestralmente. El PV total será:
La duración de Macaulay es entonces
-
 .
.
La fórmula simple encima de da (y/k =. 04/2 =. 02, c/k = 20/2 = 10):
La duración modificada, medida como porcentaje de cambio en el precio por un porcentaje punto de cambio en el rendimiento, es:
-
 (cambio % en precio por 1 porcentaje punto de cambio en el rendimiento)
(cambio % en precio por 1 porcentaje punto de cambio en el rendimiento)
DV01, medido como el cambio del dólar en el precio de un bono nominal de $100 para un cambio de punto de un porcentaje de rendimiento, es
-
 ($ por cambio de punto de 1 porcentaje en rendimiento)
($ por cambio de punto de 1 porcentaje en rendimiento)
donde la división por 100 porque modifica la duración es el porcentaje de cambio.
Duración de dólares, Bloomberg DV01, BPV, «Riesgo»
El duración de dólar o DV01 o BPV o Bloomberg Riesgo se define como negativo de la derivada del valor con respecto al rendimiento:
por lo que es el producto de la duración modificada y el precio (valor):
-
 ($ por cambio de punto de 1 porcentaje en rendimiento)
($ por cambio de punto de 1 porcentaje en rendimiento)
or
-
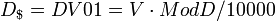 ($ cambio de 1 punto de base en el rendimiento)
($ cambio de 1 punto de base en el rendimiento)
El DV01 es análoga al delta en derivado de la fijación de precios (los griegos): es el cociente de un cambio de precio en la salida (dólares) a cambio de la unidad de entrada (un punto de base de rendimiento). Duración de dólar o DV01 es el cambio de precio en dólares, no en porcentaje. Da la variación del dólar en el valor de un bono por unidad de cambio en el rendimiento. Es a menudo medido 1 punto de base - DV01 es abreviatura de "valor en dólares de un 01" (o 1 punto de base). El nombre de BPV (valor en puntos base) o Bloomberg "Riesgo" también se utiliza, aplicado a menudo al cambio del dólar de $100 valor nominal para 100bp cambio en rendimiento - dando las mismas unidades que la duración. PV01 (valor actual de una 01) se utiliza a veces, aunque PV01 con mayor precisión se refiere al valor de un dólar o anualidad de un punto de base. (Para un bono par y un piso curva de rendimiento DV01, derivado del rendimiento precio w.r.t. y PV01, valor de una anualidad de un dólar, realmente tendrán el mismo valor.[citación necesitada])
DV01 o dólar duración puede utilizarse para instrumentos con valor inicial cero como swaps de tasas de interés donde los cambios de porcentaje y duración modificada son menos útiles.
Aplicación al valor en riesgo (VaR)
Duración de dólar  se utiliza comúnmente para valor en riesgo Cálculo (VaR). Para ilustrar aplicaciones de gestión de riesgos de cartera, considere un portafolio de valores depende de las tasas de interés
se utiliza comúnmente para valor en riesgo Cálculo (VaR). Para ilustrar aplicaciones de gestión de riesgos de cartera, considere un portafolio de valores depende de las tasas de interés  como factores de riesgo y que
como factores de riesgo y que
denotar el valor de dicha cartera. Entonces el vector de la exposición  tiene componentes
tiene componentes
En consecuencia, el cambio en el valor de la cartera se puede aproximar como
es decir, un componente que es lineal en la tasa de interés cambia más un término de error mínimo cuadrático. Esta fórmula puede utilizarse para calcular el VaR de la cartera al ignorar los términos de orden superiores. Por lo general se truncan los términos cúbicos o superiores. Cuadrática, en términos cuando incluida, puede expresarse en términos de convexidad de bonos (multi-variable). Uno puede hacer hipótesis sobre el distribución conjunta de las tasas de interés y luego calcular el VaR por Simulación Monte Carlo o, en algunos casos especiales (por ejemplo, Distribución Gausiana asumiendo una aproximación lineal), incluso analíticamente. Puede utilizarse también la fórmula para calcular el DV01 de la cartera (cf. más abajo) y puede ser generalizado para incluir los factores de riesgo más allá de las tasas de interés.
Riesgo - duración como sensibilidad de la tasa de interés
El uso principal de duración (duración modificada) es para medir la tasa de interés Incept o exposición. Pensamiento del riesgo en términos de tasas de interés o rendimientos es muy útil ya que ayuda a normalizar a través de instrumentos de otra manera dispares. Consideremos, por ejemplo, los siguientes cuatro instrumentos, cada uno con vencimiento final de 10 años:
| Descripción | Cupón ($ por año) | Precio inicial (por $100 valor nominal) | Pago final Principal | Rendimiento | Duración de Macaulay (en años) | Duración modificada (% 100bp yld ch) | BPV / DV01 ($ por 100bp yld ch) |
|---|---|---|---|---|---|---|---|
| bonos de cupón semestral 5% | $5 | $100 | $100 | 5% | años 7,99 | 7.79% | $7,79 |
| 5% anualidad semestral | $5 | $38,9729 | $0 | 5% | años 4,84 | 4.72% | $1,84 |
| bonos cupón cero | $0 | $61,0271 | $100 | 5% | 10 años | 9.76% | $5,95 |
| swap flotante fija del 5%, recepción fija | $5 | $0 | $0 | 5% | NA | NA | $7,79 |
Los cuatro tienen un vencimiento de 10 años pero la sensibilidad a las tasas de interés y, por tanto, el riesgo será diferentes: el cupón cero tiene la sensibilidad más alta y la anualidad de la más baja.
Considerar primero una inversión de $100 en cada uno, que tiene sentido para los tres bonos (bono cupón, la anualidad, los bonos cupón cero - no tiene sentido para el swap de tasa de interés que hay sin inversión inicial). Duración modificada es una medida útil para comparar la sensibilidad de la tasa de interés a través de los tres. El bono cupón cero tendrá la más alta sensibilidad, cambiando a un ritmo del 9.76% 100bp cambio en el rendimiento. Esto significa que si los rendimientos suben de 5% a 5,01% (un aumento de 1bp) el precio cayera por aproximadamente 0.0976% o un cambio en el precio de $61,0271 por cada $100 de valor nominal a aproximadamente $60,968. Original $100 invertido caerá a aproximadamente $99,90. La anualidad tiene la sensibilidad más baja, aproximadamente la mitad de los bonos cupón cero, con una duración modificada del 4,72%.
Alternativamente, podríamos considerar $100 valor nominal de cada uno de los instrumentos. En este caso el BPV o DV01 (valor en dólares de una duración de 01 o dólar) es la medida más natural. El BPV en la tabla es el cambio del dólar en el precio para $100 nominal 100bp cambio en rendimientos. El BPV hará sentido para el swap de tasa de interés (para que la duración modificada no se define) así como de los tres bonos.
Modificar las medidas de duración del tamaño de la tasa de interés Incept. A veces podemos ser engañados a pensar que mide que la parte de la curva de rendimiento del instrumento es sensible a. Después de todo, la duración modificada (% de cambio en el precio) es casi el mismo número que la duración de Macaulay (un tipo de ponderado promedio de años a la madurez). Por ejemplo, la anualidad anterior tiene una duración de Macaulay de 4,8 años y podríamos pensar que es sensible a la producción de 5 años. Pero tiene un flujo hacia fuera a 10 años y así será sensible a las producciones de 10 años. Si queremos medir la sensibilidad a las partes de la curva de rendimiento que debemos tener en cuenta duración de la tasa clave.
Obligaciones con los flujos de efectivo fijados un cambio de precio puede provenir de dos fuentes:
- El paso del tiempo (convergencia hacia la igualdad). Esto por supuesto es totalmente predecible y por lo tanto no un riesgo.
- Un cambio en el rendimiento. Esto puede ser debido a un cambio en el rendimiento de referencia y cambio en la producción de extensión.
La relación rendimiento-precio es inversa, y la duración modificada proporciona una medida muy útil de la sensibilidad del precio a los rendimientos. Como una primera derivada proporciona una aproximación lineal. Para cambios de gran rendimiento, convexidad puede añadirse para proporcionar una aproximación cuadrática o de segundo orden. Alternativamente y a menudo más provechosamente, la convexidad puede utilizarse para medir cómo la duración modificada cambios como el cambio de rendimiento. Medidas de riesgo similares (primer y segundo orden) utilizado en las opciones de los mercados son el Delta y gamma.
Duración modificada y DV01 como medida de sensibilidad de la tasa de interés también son útiles porque pueden ser aplicados a los instrumentos y títulos con flujos variables o contingentes, como las opciones.
Opciones de encajado y duración efectiva
Para los bonos que tienen Opciones de encajado, tales como bonos amortizables y computables, duración modificada correctamente no aproximar el movimiento del precio de un cambio en el rendimiento.
Para precio de dichos bonos, se debe utilizar precio de la opción para determinar el valor de los bonos y entonces uno puede computar su Delta (y por lo tanto su lambda), que es la duración. El duración efectiva es una aproximación discreta a este último y depende de una opción en el modelo de precios.
Considere un bono con una opción de venta integrado. Por ejemplo, un bono de $1.000 que puede ser canjeado por el titular a la par en cualquier momento antes del vencimiento de los bonos (es decir, un americano pone opción). No importa cómo altas tasas de interés se convierten, el precio del bono nunca pasa por debajo de $1.000 (ignorando el riesgo de contraparte). Sensibilidad al precio de este bono a los cambios de la tasa de interés es diferente de un enlace no pasivo con idéntico flujos de caja. Bonos que han incorporado opciones pueden analizarse utilizando la "duración efectiva". Duración efectiva es una aproximación discreta de la vertiente del valor del bono en función de la tasa de interés.
donde Δy es la cantidad que producen cambios, y
son los valores que tendrá el bono si el rendimiento cae por y o se levanta por y, respectivamente. Sin embargo este valor variará según el valor utilizado para Δy.
Duración de la propagación
Sensibilidad del precio de mercado de un bono a un cambio en Opción ajusta extensión (OEA). Así el índice, o curva de rendimiento subyacente, permanece sin cambios. Flotante de activos de tasa que están referenciados a un índice (por ejemplo, LIBOR 1 mes o 3 meses) y se restablece periódicamente tendrán una duración efectiva cerca de cero pero una duración de extensión comparable a un bono de tasa fija idéntico.
Duración media
La sensibilidad de un cartera de de bonos como un vínculo fondo mutuo a los cambios en las tasas de interés también pueden ser importantes. La duración media de los bonos en la cartera se divulga a menudo. La duración de una cartera es igual a la madurez de promedio ponderada de todos los flujos de efectivo en la cartera. Si cada enlace tiene el mismo rendimiento al vencimiento, esto es igual a la media ponderada de las duraciones de los bonos de la cartera, con pesos proporcionales a los precios de los bonos.[1] De lo contrario el promedio ponderado de las duraciones de la Unión es sólo una buena aproximación, pero todavía puede ser utilizado para inferir cómo cambiaría el valor de la cartera en respuesta a cambios en las tasas de interés.
Convexidad
Duración es un lineal medida de cómo el precio de un bono cambia en respuesta a los cambios de la tasa de interés. Como las tasas de interés cambian, el precio no cambia linealmente, sino que es un función convexa de las tasas de interés. Convexidad es una medida de la curvatura de cómo cambia el precio de un bono como los cambios de la tasa de interés. Específicamente, la duración puede ser formulada como el primer derivado de la de la función de precio del bono con respecto a la tasa de interés en cuestión y la convexidad como la segunda derivada.
La convexidad también da una idea de la difusión de flujos de caja futuros. (Así como la duración da el término medio con descuento, así que la convexidad puede utilizarse para calcular la desviación estándar con descuento, digo, de vuelta.)
Tenga en cuenta que la convexidad puede ser positiva o negativa. Un vínculo con convexidad positiva no tendrá las características de la llamada - es decir, el emisor debe canjear el bono en la madurez - que significa que como las tasas de caída, su duración y el precio subirá.
Por el contrario, un vínculo con características de llamada - es decir, donde el emisor puede redimir el vínculo temprano - se considera que convexidad negativa Cuando las tasas acercan el strike de la opción, es decir su duración caerá como tasas de caída, y por lo tanto, su precio subirá menos rápidamente. Esto es porque el emisor puede redimir el bono viejo a un cupón alto y vuelva a emitir un nuevo bono a una tasa menor, proporcionando así el emisor con opcionalidad valiosa.
Valores respaldados por hipotecas (hipoteca paso principales pagos por adelantado) con 15 o 30 años estilo fijo hipotecas como garantía son ejemplos de bonos amortizables.
Véase también
- Valoración de bonos
- Inmunización (finanzas)
- Duración acción
- Convención de la cuenta del día
- Lista de temas de finanzas
Notas
Referencias
- ^ a b c d Hull, John C. (1993), Opciones, futuros y otros valores derivados (Segunda ed.), Englewood Cliffs, NJ: Prentice-Pasillo, Inc., pp. 99 – 101
- ^ a b Brealey, Richard A.; Myers, Stewart C.; Allen, Franklin (2011), Principios de finanzas corporativas (Décima ed.), New York, NY: McGraw-Hill Irwin, pp. 50 – 53
- ^ a b c Coleman, Thomas. "Una guía a duración, DV01 y transformaciones de riesgo de curva de rendimiento". Red de investigación de ciencias sociales. 22 de enero 2013.
- ^ Cuando los rendimientos se agravan continuamente duración de Macaulay y la duración modificada será numéricamente igual. Cuando los rendimientos se agravan periódicamente Macaulay y la duración modificada serán ligeramente diferente, y existe una relación simple entre los dos.
- ^ Marrison, Chris (2002), Los fundamentos de la medición del riesgo, Boston, MA: McGraw-Hill, págs. 57 – 58
- ^ Berk, Jonathan; DeMarzo, Peter (2011), Finanzas corporativas (Segunda ed.), Boston, MA: Prentice Hall, págs. 966-969
- ^ "Duración de Macaulay«por Fiona Maclachlan, El proyecto de demostraciones Wolfram.
- ^ "lidiar con el riesgo de las fluctuaciones de la tasa de interés: devuelve a los tenedores de bonos de ingenua y óptimas estrategias." Lawrence Fisher y Roman L. Weil; Diario de negocios, 1971, 44(4), pp. 408-31. https://links.JSTOR.org/Sici?Sici=0021-9398%28197110%2944%3A4%3C408%3ACWTROI%3E2.0.co%3b2-%23
- ^ Ho, Thomas S.Y. (septiembre de 1992). "clave tasa duración: medidas de los riesgos de tasa de interés". Diario de renta fija 2 (2): 29-44.
- ^ Reitano, Robert R. (enero de 1991). "Análisis multivariante duración" (PDF). Transacciones de la sociedad de actuarios. XLIII: 335 – 391. de 2011.
- ^ Reitano, Robert R. (2008). Fabozzi, Frank J., ed. "rendimiento curva Risk Management". Manual de finanzas (Hoboken, NJ: Juan Wiley e hijos) 3: 215.
- ^ Body; Kane; Marcus (1993), Inversiones (Segunda ed.), p. 478
Lectura adicional
- Fabozzi, Frank J. (1999), "Los fundamentos de duración y convexidad", Duración, convexidad y otras medidas de riesgo de bonos, Serie de Fabozzi Frank J. 58, Juan Wiley e hijos, ISBN9781883249632
- Mayle, Jan (1994), Valores estándar métodos de cálculo: Fórmulas de valores de renta fija medidas analíticas 2 (1ª ed.), Securities Industry and Financial Markets Association, ISBN1-882936-01-9. La referencia estándar para convenios aplicables a los valores estadounidenses.
Acoplamientos externos
- Enciclopedia de riesgo para una buena explicación en las múltiples definiciones de duración y sus orígenes.
- Explicación de duración de investopedia
|
||||||||||||||||||||||||||||||


 es el tiempo en años, hasta el
es el tiempo en años, hasta el 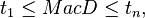


 es el flujo de efectivo de la
es el flujo de efectivo de la 

 .
.





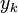 es el rendimiento al vencimiento de un activo, agravado periódicamente
es el rendimiento al vencimiento de un activo, agravado periódicamente
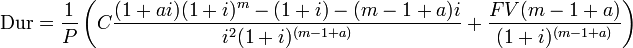
![MacD = \left[ \frac {(1+y/k)}{y/k} - \frac {100(1+y/k)+m(c/k-100y/k)}{(c/k)[(1+y/k)^m-1]+100y/k} \right ] / k](http://upload.wikimedia.org/math/c/4/c/c4cf99bd5c06c34db91ac4e4b5b0da25.png)


 .
.
![MacD = \left[ \frac {(1.02)}{0.02} - \frac {100(1.02)+4(10-2)}{10[(1.02)^{4}-1]+2} \right] / 2 = 1.777 years](http://upload.wikimedia.org/math/8/d/d/8dda9cc5b196756e65be0b05bd5ab0ff.png)
 (cambio % en precio por 1 porcentaje punto de cambio en el rendimiento)
(cambio % en precio por 1 porcentaje punto de cambio en el rendimiento)
 ($ por cambio de punto de 1 porcentaje en rendimiento)
($ por cambio de punto de 1 porcentaje en rendimiento)

 ($ por cambio de punto de 1 porcentaje en rendimiento)
($ por cambio de punto de 1 porcentaje en rendimiento)
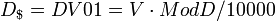 ($ cambio de 1 punto de base en el rendimiento)
($ cambio de 1 punto de base en el rendimiento)




