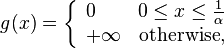Entrópico valor en riesgo
En matemáticas financieras y Optimización Estocástica, el concepto de medida del riesgo se utiliza para cuantificar el riesgo de un resultado aleatorio o posición del riesgo. Hasta ahora se han propuesto muchas medidas de riesgo, cada uno con ciertas características. El entrópico value-at-risk (EVaR) es un medida de riesgo coherente introducido por Ahmadi-Javid,[1][2] que es un límite superior para el valor en riesgo (VaR) y la valor en riesgo condicional (CVaR), obtenidos de la Desigualdad Chernoff. El EVaR también puede ser representado mediante el uso del concepto de entropía relativa. Debido a su conexión con el VaR y la entropía relativa, esta medida del riesgo se llama "entrópico value-at-risk". El EVaR fue desarrollado para hacer frente a algunas ineficiencias computacionales[aclaración necesitado] de la variable. Obtener inspiración de la representación dual de la EVaR, Ahmadi-Javid[1][2] desarrollado una amplia clase de medidas de riesgo coherentes, llamado medidas de riesgo g-entrópico. El CVaR tanto el EVaR son miembros de esta clase.
Contenido
- 1 Definición
- 2 Propiedades
- 3 Ejemplos
- 4 Optimización
- 5 Generalización (medidas de riesgo g-entrópico)
- 6 Véase también
- 7 Referencias
Definición
Dejar  ser un espacio probabilístico con
ser un espacio probabilístico con  un conjunto de todos los eventos simples,
un conjunto de todos los eventos simples,  un
un  -Álgebra de subconjuntos de
-Álgebra de subconjuntos de  y
y  un medida de la probabilidad en
un medida de la probabilidad en  . Dejar
. Dejar  ser un variable aleatoria y
ser un variable aleatoria y  el conjunto de todos Borel mensurable funciones
el conjunto de todos Borel mensurable funciones  cuyo Función generadora de momento
cuyo Función generadora de momento  existe para todos
existe para todos  . La entrópica value-at-risk (EVaR) de
. La entrópica value-at-risk (EVaR) de  con nivel de confianza
con nivel de confianza  se define como sigue:
se define como sigue:
-

(1)
En finanzas, el variable aleatoria  , en la ecuación anterior, se utiliza al modelo de la pérdidas de una cartera.
, en la ecuación anterior, se utiliza al modelo de la pérdidas de una cartera.
Considerar la desigualdad Chernoff
-

(2)
Resolviendo la ecuación 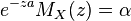 para
para  , resulta en
, resulta en  . Teniendo en cuenta la ecuación)1), vemos que
. Teniendo en cuenta la ecuación)1), vemos que  , que muestra la relación entre el EVaR y la desigualdad Chernoff. Es importante destacar
, que muestra la relación entre el EVaR y la desigualdad Chernoff. Es importante destacar 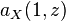 es el medida del riesgo entrópica o exponencial premium, que es un concepto usado en finanzas y seguros, respectivamente.
es el medida del riesgo entrópica o exponencial premium, que es un concepto usado en finanzas y seguros, respectivamente.
Dejar 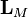 el conjunto de todas las funciones medibles de Borel
el conjunto de todas las funciones medibles de Borel  cuya función generadora de momento
cuya función generadora de momento  existe para todos
existe para todos  . El representación doble (o representación sólida) de la EVaR es como sigue:
. El representación doble (o representación sólida) de la EVaR es como sigue:
-

(3)
donde  , y
, y  es un conjunto de medidas de probabilidad en
es un conjunto de medidas de probabilidad en  con
con  . Tenga en cuenta que
. Tenga en cuenta que  es el entropía relativa de
es el entropía relativa de  con respecto a
con respecto a  , también llamado el Divergencia de Kullback-Leibler. La representación dual de la EVaR revela el motivo de su nombramiento.
, también llamado el Divergencia de Kullback-Leibler. La representación dual de la EVaR revela el motivo de su nombramiento.
Propiedades
- El EVaR es una medida de riesgo coherente.
- La función generadora de momento
 puede ser representado por el EVaR: para todos
puede ser representado por el EVaR: para todos  y
y 
-

(4)
- Para
 ,
,  para todos
para todos ![\alpha\in]0,1]](//upload.wikimedia.org/math/4/1/5/41566895bbfef7e581895b15a38c2805.png) Si y sólo si
Si y sólo si 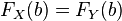 para todos
para todos  .
. - La medida del riesgo entrópica con parámetro
 , puede ser representado mediante el EVaR: para todos
, puede ser representado mediante el EVaR: para todos  y
y 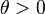
-

(5)
- El EVaR con nivel de confianza
 es el límite superior posible más apretado que pueden obtenerse de la desigualdad Chernoff para el VaR y el CVaR con nivel de confianza
es el límite superior posible más apretado que pueden obtenerse de la desigualdad Chernoff para el VaR y el CVaR con nivel de confianza  ;
;
-

(6)
- La desigualdad siguiente depara el EVaR:
-

(7)
donde 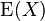 es el valor esperado de
es el valor esperado de  y
y  es el supremum esencial de
es el supremum esencial de  , es decir,
, es decir,  . Así que no
. Así que no  y
y  .
.
Ejemplos
Para 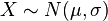 ,
,
-
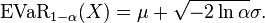
(8)
Para 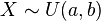 ,
,
-

(9)
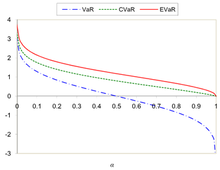
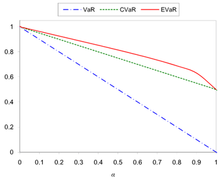
Las figuras 1 y 2 muestran la comparación del VaR, CVaR y EVaR para  y
y  .
.
Optimización
Dejar  ser una medida de riesgo. Considerar el problema de optimización
ser una medida de riesgo. Considerar el problema de optimización
-

(10)
donde 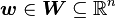 es un
es un  -dimensional real vector de decisión,
-dimensional real vector de decisión, 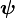 es un
es un  -dimensional real vector aleatorio con un conocido distribución de probabilidad y la función
-dimensional real vector aleatorio con un conocido distribución de probabilidad y la función  es una función medible Borel para todos los valores
es una función medible Borel para todos los valores  . If
. If  es el
es el 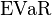 , entonces el problema (10) se convierte como sigue:
, entonces el problema (10) se convierte como sigue:
-

(11)
Dejar  ser el soporte del vector aleatorio
ser el soporte del vector aleatorio 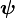 . If
. If 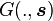 es convexo para todos
es convexo para todos  , entonces la función objetivo de la (problema11) también es convexo. If
, entonces la función objetivo de la (problema11) también es convexo. If  tiene la forma
tiene la forma
-

(12)
y  son variables aleatorias independientes en
son variables aleatorias independientes en  , entonces ()11) se convierte en
, entonces ()11) se convierte en
-
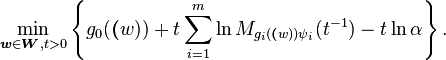
(13)
que es computacionalmente manejable. Pero para este caso, si uno utiliza el CVaR en problema (10), entonces el problema resultante se convierte como sigue:
-
![\min_{\boldsymbol{w}\in\boldsymbol{W}, t\in\R}\left\lbrace
t+\frac{1}{\alpha}\text{E}\left[
g_0(\boldsymbol{w})+\sum_{i=1}^{m}g_i(\boldsymbol{w})
\psi_i-t
\right]_+
\right\rbrace.\,](//upload.wikimedia.org/math/e/e/9/ee9f8d0962de19d1dc9837ec79672c1e.png)
(14)
Puede ser demostrado al aumentar la dimensión de  , (problema14) es computacionalmente intratable incluso para casos sencillos. Por ejemplo, supongamos
, (problema14) es computacionalmente intratable incluso para casos sencillos. Por ejemplo, supongamos  son independientes variables aleatorias discretas esa toma
son independientes variables aleatorias discretas esa toma  valores distintos. Para valores fijos de
valores distintos. Para valores fijos de  y
y  , la complejidad de la función objetivo dada en (problema de computación13) es de orden
, la complejidad de la función objetivo dada en (problema de computación13) es de orden  mientras el tiempo de computación para la función objetivo del problema)14) es de orden
mientras el tiempo de computación para la función objetivo del problema)14) es de orden  . Por ejemplo, asuma que
. Por ejemplo, asuma que 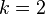 ,
, 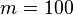 y lleva a la suma de dos números
y lleva a la suma de dos números  segundos. Para calcular la función objetivo del problema)14) uno necesita sobre
segundos. Para calcular la función objetivo del problema)14) uno necesita sobre  años, considerando que la evaluación de la función objetivo del problema ()13) tarda aproximadamente
años, considerando que la evaluación de la función objetivo del problema ()13) tarda aproximadamente 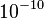 segundos. Esto demuestra que la formulación con la EVaR supera la formulación con el CVaR (véase [2] para más detalles).
segundos. Esto demuestra que la formulación con la EVaR supera la formulación con el CVaR (véase [2] para más detalles).
Generalización (medidas de riesgo g-entrópico)
Inspirándose en la representación dual de la EVaR dada en)3), se puede definir una amplia clase de medidas de riesgo coherentes información teórica, que se introducen en.[1][2] Dejar  ser una convexa funcionamiento con
ser una convexa funcionamiento con  y
y  ser un número no negativo. El
ser un número no negativo. El  -medida del riesgo entrópica con nivel de divergencia
-medida del riesgo entrópica con nivel de divergencia  se define como
se define como
-

(15)
donde 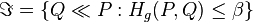 en el cual
en el cual 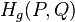 es el entropía generalizada relativa de
es el entropía generalizada relativa de  con respecto a
con respecto a  . Una representación primitiva de la clase de
. Una representación primitiva de la clase de  -medidas de riesgos antrópicos pueden obtenerse de la siguiente manera:
-medidas de riesgos antrópicos pueden obtenerse de la siguiente manera:
-
![\text{ER}_{g,\beta}(X)=\inf_{t>0,\mu\in\R}\left\lbrace
t\left[
\mu+\text{E}_P\left(
g^*\left(
\frac{X}{t}-\mu+\beta
\right)
\right)
\right]
\right\rbrace\,](//upload.wikimedia.org/math/e/8/5/e8550c8b18a19f3a4f5df9f28856fbe1.png)
(16)
donde 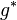 es el conjugado de
es el conjugado de  . Teniendo en cuenta
. Teniendo en cuenta
-

(17)
con  y
y  , se deduce la fórmula EVaR. El CVaR es también un
, se deduce la fórmula EVaR. El CVaR es también un  -medida del riesgo entrópico, que puede obtenerse en ()16) mediante el establecimiento de
-medida del riesgo entrópico, que puede obtenerse en ()16) mediante el establecimiento de
-
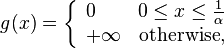
(18)
con 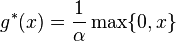 y
y 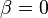 (véase [1][3] para más detalles).
(véase [1][3] para más detalles).
Para obtener más resultados en  -Ver medidas de riesgos antrópicos.[4]
-Ver medidas de riesgos antrópicos.[4]
Véase también
- Optimización Estocástica
- Medida del riesgo
- Medida de riesgo coherente
- Valor en riesgo
- Valor en riesgo condicional
- Déficit esperado
- Medida del riesgo entrópica
- Divergencia de Kullback-Leibler
- Entropía generalizada relativa
Referencias
- ^ a b c d Ahmadi-Javid, Amir (2011). Un enfoque teórico-información para construir medidas de riesgo coherentes. San Petersburgo, Rusia: Actas de IEEE International Symposium on teoría de la información. 2125 pp. – 2127. Doi:10.1109/ISIT.2011.6033932.
- ^ a b c d Ahmadi-Javid, Amir (2012). "Value-at-risk entrópico: una nueva medida de riesgo coherente". Diario de optimización teoría y aplicaciones 155 (3): 1105-1123. Doi:10.1007/s10957-011-9968-2.
- ^ Ahmadi-Javid, Amir (2012). "Adenda: entrópico Value-at-Risk: una nueva medida de riesgo coherente". Diario de optimización teoría y aplicaciones 155 (3): 1124-1128. Doi:10.1007/s10957-012-0014-9.
- ^ Breuer, Thomas; Csiszar, Imre (2013). "Medición de riesgo del modelo de distribución". arXiv:1301.4832v1.





 ,
,  para todos
para todos ![\alpha\in]0,1]](http://upload.wikimedia.org/math/4/1/5/41566895bbfef7e581895b15a38c2805.png) Si y sólo si
Si y sólo si 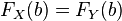 para todos
para todos  .
. , puede ser representado mediante el EVaR: para todos
, puede ser representado mediante el EVaR: para todos 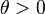



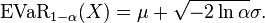




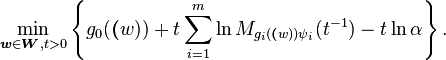
![\min_{\boldsymbol{w}\in\boldsymbol{W}, t\in\R}\left\lbrace
t+\frac{1}{\alpha}\text{E}\left[
g_0(\boldsymbol{w})+\sum_{i=1}^{m}g_i(\boldsymbol{w})
\psi_i-t
\right]_+
\right\rbrace.\,](http://upload.wikimedia.org/math/e/e/9/ee9f8d0962de19d1dc9837ec79672c1e.png)

![\text{ER}_{g,\beta}(X)=\inf_{t>0,\mu\in\R}\left\lbrace
t\left[
\mu+\text{E}_P\left(
g^*\left(
\frac{X}{t}-\mu+\beta
\right)
\right)
\right]
\right\rbrace\,](http://upload.wikimedia.org/math/e/8/5/e8550c8b18a19f3a4f5df9f28856fbe1.png)