Haven (teoría de gráfico)
En teoría de grafos, un Haven es un cierto tipo de función en conjuntos de vértices en un gráfico sin señas. Si existe un refugio, puede ser utilizado por un evasor para ganar un persecución-evasión el gráfico, consultando a la función en cada paso del juego para determinar un sistema seguro de vértices para entrar en el juego. Los paraísos se introdujeron por primera vez Seymour & Thomas (1993) como una herramienta para la caracterización de la treewidth de gráficos.[1] Sus otros usos incluyen probar la existencia de separadores de pequeños en familias cerrado menor de gráficos,[2] y caracterizar el extremos y camarilla menores de edad de gráficos infinitos.[3][4]
Contenido
- 1 Definición
- 2 Ejemplo
- 3 Persecución-evasión
- 4 Conexiones treewidth, separadores y menores
- 5 En gráficos infinitos
- 6 Referencias
Definición
If G es un gráfico sin señas, y X es un conjunto de vértices, y luego un X-aleta es una no vacía componente conectado de la subgráfico de G formado por eliminar X. A Haven de la orden k en G es una función β que asigna un X-aleta β(X) para cada sistema X de menos de k vértices. Esta función también debe satisfacer las limitaciones adicionales que se dan en forma diferente por diversos autores. El número de k se llama el orden del asilo.[5]
En la definición original de Seymour y Thomas,[1] un refugio es necesario para satisfacer la propiedad que cada dos aletas β(X) y β(Y) deben tocarse: comparten un vértice común o existe una arista con un extremo en cada aleta. En la definición utilizada luego por Alon, Seymour y Thomas,[2] paraísos en cambio están obligados a satisfacer una débil moniticidad propiedad: Si X ⊆ Yy ambos X y Y tiene menos de k vértices, entonces β(Y) ⊆ β(X). La conmovedora propiedad implica la propiedad moniticidad, pero no necesariamente al revés. Sin embargo, se desprende de los resultados de Seymour y Thomas[1] que, en los gráficos finitos, si existe un refugio con la propiedad moniticidad, entonces uno con el mismo orden y la propiedad conmovedor también existe.

Los paraísos con la emotiva definición están estrechamente relacionados con Brambles, familias de subgráficos conectados de un grafo dado que todos tocan entre sí. El orden de una zarza es el mínimo número de vértices necesarios en un conjunto de vértices que afecta a todos los subgráficos en la familia. El conjunto de aletas β(X) para un refugio de la orden k (con la emotiva definición) forma una zarza de orden al menos k, porque cualquier conjunto Y de menos de k vértices no logra golpear el subgráfico β(Y). Por el contrario, de cualquier Zarza de orden k, uno puede construir un refugio de la misma orden, definiendo β(X) (para cada opción de X) para ser el X-aleta que incluye todos los subgráficos en la zarza que están separados deX. El requisito de que los subgráficos en la zarza todos tocan entre sí puede utilizarse para demostrar que esto X-aleta existe y que todas las aletas β(X) elegido de esta manera toca entre sí. Así, un gráfico tiene una zarza de orden k Si y sólo si cuenta con un refugio de la ordenk.
Ejemplo
Como ejemplo, que G ser un nueve-vértice gráfico de la rejilla. Definir un remanso de orden 4 G, mapeo de cada sistema X de los vértices de tres o menos a un X-aleta β(X), como sigue:
- Si hay un único X-aleta es más grande que cualquiera de las otras X-Deja que las aletas, β(X) que ser único grande X-aleta.
- En caso contrario, elija β(X) arbitrariamente a cualquiera X-aleta.
Es fácil de comprobar por un Análisis de caso que esta función β satisface la propiedad de moniticidad requiere de un refugio. If X ⊆ Y y X tiene al menos dos vértices, o X tiene dos vértices que no los dos vecinos de un vértice de la esquina de la cuadrícula, entonces sólo hay uno X-aleta y contiene todos los Y-aleta. En el caso restante, X consta de los dos vecinos de un vértice de la esquina y tiene dos X-aletas: uno consiste en ese vértice de la esquina y otro (elegido como β(X)) que consta de los seis restantes vértices. Sin importar cuál vértice se agrega a X para formar Y, habrá un Y-aleta con por lo menos cuatro vértices, que debe ser la única aleta más grande ya que contiene más de la mitad de los vértices no Y. Este gran Y-aleta será elegida como β(Y) y será un subconjunto de β(X). Así en cada caso moniticidad lleva a cabo.
Persecución-evasión
Los paraísos modelo cierta clase de estrategias para un evasor en un persecución-evasión juego en el que menos de k perseguidores intentan capturar un evasor sola, los perseguidores y evasores son ambos restricción a los vértices de un grafo dado sin señas, y las posiciones de los perseguidores y evasores son conocidas por ambos jugadores. En cada jugada del partido, un nuevo perseguidor puede agregarse a un vértice del gráfico (como durante mucho tiempo como menos arbitrario k sus perseguidores se colocan en el gráfico en cualquier momento) o uno de los perseguidores ya agregado puede ser removido de la gráfica. Sin embargo, antes de añade un nuevo perseguidor, el evasor es informado primero de su nueva ubicación y podrá moverse a lo largo de los bordes del gráfico para cualquier vértice desocupado. Mientras se mueve, el evasor no puede pasar por cualquier vértice que está ya ocupado por cualquiera de los perseguidores.
Si un k-asilo (con la propiedad moniticidad) existe, entonces el evasor puede evitar ser capturado indefinidamente y ganar el juego, moviendo siempre a un vértice del β(X) donde X es el conjunto de vértices que serán ocupadas por sus perseguidores al final de la jugada. La propiedad moniticidad de un refugio garantiza que, cuando un nuevo perseguidor se agrega a un vértice del gráfico, los vértices en β(X) siempre son accesibles desde la posición actual de los evasores.[1]
Por ejemplo, un evasor puede ganar este partido contra tres perseguidores en una 3 × 3 red siguiendo esta estrategia con el asilo de orden descrito en el ejemplo 4. Sin embargo, en el mismo gráfico, cuatro perseguidores siempre captura el evasor, primera mudanza en tres vértices que dividir la red en dos rutas de acceso de tres vértices, y luego entrando en el centro de la ruta de acceso que contiene el evasor, obligando a los evasores a uno de los vértices de la esquina y finalmente eliminar uno de los perseguidores que no está adyacente a este rincón y apoyándolo sobre el evasor. Por lo tanto, la 3 × 3 la red no puede tener ningún refugio de orden 5.
Los paraísos con la propiedad conmovedor permiten el evasor ganar el partido contra sus perseguidores más poderosos que puede saltar desde un conjunto de vértices ocupados simultáneamente a otro.[1]
Conexiones treewidth, separadores y menores
Los paraísos pueden utilizarse para caracterizar la treewidth de gráficos: un gráfico tiene un refugio de la orden k Si y sólo si tiene por lo menos treewidth k − 1. La descomposición de un árbol puede utilizarse para describir una estrategia ganadora para los perseguidores en el mismo juego de persecución-evasión, así que también es cierto que un gráfico tiene un refugio de la orden k Si y sólo si gana el evasor con mejor jugar contra menos de k perseguidores. En juegos ganados por el evasor, siempre hay una estrategia óptima en la forma descrita por un refugio, y en juegos ganados por el perseguidor, siempre hay una estrategia óptima en la forma descrita por la descomposición de un árbol.[1] Por ejemplo, porque el 3 × 3 rejilla tiene un refugio de orden 4, pero no tiene un refugio de orden 5, debe tener treewidth exactamente 3. El mismo Teorema de min-max se puede generalizar a gráficos infinitos de treewidth finito, con una definición de treewidth en que el árbol subyacente es necesaria para ser rayless (que es, no tener extremos).[1]
Los paraísos están también estrechamente relacionados con la existencia de separadores, pequeños conjuntos X vértices en un n-gráfico de vértice tal que cada X-aleta tiene a lo sumo 2n/ 3 vértices. If un gráfico G No tiene un k-separador de vértice, entonces cada set X de a lo más k vértices tiene un (único) X-aleta con más de 2n/ 3 vértices. En este caso, G tiene un refugio de la orden k + 1, en el cual β(X) se define como este único grande X-aleta. Es decir, cada gráfico tiene un separador pequeño o un refugio de orden superior.[2]
If un gráfico G tiene un refugio de la orden k, con k ≥ h3/2n1/2 para algunos enteros h, entonces G también debe tener un grafo completo Kh como un Minor. En otras palabras, la Número de Hadwiger de un n-gráfico de vértice con un refugio de la orden k es por lo menos k2/3n−1/3. Como consecuencia, la Kh-menor-gráficos gratis que treewidth menos h3/2n1/2 y separadores de tamaño inferior a h3/2n1/2. Más generalmente una O (√n) límite de tamaño treewidth y separador sostiene para cualquier familia no trivial de gráficos que se caracteriza por prohibido menores, porque para cualquier familia tan hay una constante h tal que la familia no incluye Kh.[2]
En gráficos infinitos
If un gráfico G contiene un rayo, un trazado simple semi-infinita con un vértice de partida pero no vértice final, entonces tiene un refugio de la orden ℵ0:: es decir, una función β que los mapas cada conjunto finito X de los vértices de un X-aleta, satisfaciendo la condición de consistencia para refugios. Es decir, definir β(X) sea el único X-solapa que contiene infinitamente muchos vértices del rayo. Así, en el caso de gráficos infinitos se rompe la conexión entre treewidth y los paraísos: un rayo de luz, a pesar de sí mismo siendo un árbol, tiene los paraísos de todas las órdenes finitos y aún más fuertemente un remanso de orden ℵ0. Dos rayos de un gráfico de infinito se consideran equivalentes si no hay ningún conjunto finito de los vértices que se separa infinitamente muchos vértices de una rayo de infinitamente muchos vértices del otro rayo; se trata de un relación de equivalenciay su clases de equivalencia se llaman extremos del gráfico.
Los extremos de cualquier gráfico están en correspondencia uno a uno con sus paraísos de orden ℵ0. Cada rayo determina un refugio, y cada dos rayos equivalentes determinan el asilo de la mismo.[3] Por el contrario, cada asilo está determinada por un rayo de esta manera, como puede ser demostrado por el análisis de casos siguiente:
- Si el asilo tiene la propiedad que la intersección
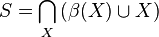 (donde la intersección se extiende sobre todos los conjuntos finitos X) es en sí mismo un conjunto infinito S, entonces todos los finito simple camino que termina en un vértice del S puede ser extendido para llegar a un vértice adicional de S, y repitiendo este proceso de extensión produce un rayo atravesando infinitamente muchos vértices de S. Este rayo determina el asilo dado.
(donde la intersección se extiende sobre todos los conjuntos finitos X) es en sí mismo un conjunto infinito S, entonces todos los finito simple camino que termina en un vértice del S puede ser extendido para llegar a un vértice adicional de S, y repitiendo este proceso de extensión produce un rayo atravesando infinitamente muchos vértices de S. Este rayo determina el asilo dado. - Por otro lado, si S es finito, entonces (por trabajar en el subgráfico G\S) puede ser asumido que para estar vacío. En este caso, para cada conjunto finito Xi es un conjunto de vértices Xi+ 1 con la propiedad que Xi está desunido de
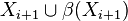 . Si un ladrón sigue la estrategia de evasión determinada por el asilo, y la policía sigue una estrategia dada por esta secuencia de conjuntos, entonces la ruta seguida por el ladrón forma un rayo que determina el asilo.[4]
. Si un ladrón sigue la estrategia de evasión determinada por el asilo, y la policía sigue una estrategia dada por esta secuencia de conjuntos, entonces la ruta seguida por el ladrón forma un rayo que determina el asilo.[4]
Así, cada clase de equivalencia de rayos define un refugio único y cada asilo está definido por una clase de equivalencia de los rayos.
Para cualquier número cardinal 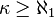 , un gráfico de infinito G tiene un remanso de orden κ si y sólo si tiene un camarilla Minor de orden κ. Es decir, para incontables cardinalities, el mayor pedido de un refugio en G es el Número de Hadwiger de G.[3]
, un gráfico de infinito G tiene un remanso de orden κ si y sólo si tiene un camarilla Minor de orden κ. Es decir, para incontables cardinalities, el mayor pedido de un refugio en G es el Número de Hadwiger de G.[3]
Referencias
- ^ a b c d e f g Seymour, Paul D.; Thomas, Robin (1993), "ámbito gráfico y un teorema de min-max para árbol de ancho", Revista de teoría combinatoria, serie B 58 (1): 22 – 33, Doi:10.1006/jctb.1993.1027.
- ^ a b c d Alon, Noga; Seymour, Paul; Thomas, Robin (1990), «Un teorema separador para extrusión gráficos», J. Amer. matemáticas. Soc. 3 (4): 801-808, Doi:10.1090/S0894-0347-1990-1065053-0.
- ^ a b c Robertson, Neil; Seymour, Paul; Thomas, Robin (1991), "excepto los menores infinitos", Matemáticas discretas 95 (1-3): 303-319, Doi:10.1016/0012-365 X 90343-Z (91), MR1141945.
- ^ a b Diestel, Reinhard; Kühn, Daniela (2003), "Gráfico-teórico versus extremos topológicos de gráficos", Revista de teoría combinatoria, Serie B 87 (1): 197-206, Doi:10.1016/S0095-8956 (02) 00034-5, MR1967888.
- ^ Johnson, Thor.; Robertson, Neil.; Seymor, P.D.; Thomas, Robin (2001), "árbol ancho dirigida", Revista de teoría combinatoria, serie B 82 (1): 138 – 155, Doi:10.1006/jctb.2000.2031.
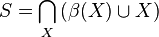 (donde la intersección se extiende sobre todos los conjuntos finitos X) es en sí mismo un conjunto infinito S, entonces todos los finito simple camino que termina en un vértice del S puede ser extendido para llegar a un vértice adicional de S, y repitiendo este proceso de extensión produce un rayo atravesando infinitamente muchos vértices de S. Este rayo determina el asilo dado.
(donde la intersección se extiende sobre todos los conjuntos finitos X) es en sí mismo un conjunto infinito S, entonces todos los finito simple camino que termina en un vértice del S puede ser extendido para llegar a un vértice adicional de S, y repitiendo este proceso de extensión produce un rayo atravesando infinitamente muchos vértices de S. Este rayo determina el asilo dado.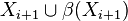 . Si un ladrón sigue la estrategia de evasión determinada por el asilo, y la policía sigue una estrategia dada por esta secuencia de conjuntos, entonces la ruta seguida por el ladrón forma un rayo que determina el asilo.
. Si un ladrón sigue la estrategia de evasión determinada por el asilo, y la policía sigue una estrategia dada por esta secuencia de conjuntos, entonces la ruta seguida por el ladrón forma un rayo que determina el asilo.