Número cardinal

Este artículo es sobre el concepto matemático. Para número de palabras que indican cantidad (manzanas "tres", "cuatro" pájaros, etc.), consulte Número cardinal (lingüística).

Una función biyectiva, f: X → Y, del conjunto X para establecer Y demuestra que los conjuntos tienen la misma cardinalidad, en este caso igual que el cardenal número 4.

Aleph nulo, el cardenal infinito más pequeño

En matemáticas, números cardinales, o cardenales para abreviar, es una generalización de la números naturales utilizado para medir la Cardinalidad (tamaño) de establece. La cardinalidad de un conjunto finito es un número natural – el número de elementos en el conjunto. El Transfinito números cardinales describir los tamaños de conjuntos infinitos.

Cardinalidad se define en términos de funciones biyectiva. Dos conjuntos tienen la misma cardinalidad si y sólo si hay una correspondencia uno a uno (biyección) entre los elementos de los dos conjuntos. En el caso de conjuntos finitos, esto coincide con la noción intuitiva de tamaño. En el caso de series infinitas, el comportamiento es más complejo. Un Teorema fundamental debido a Georg Cantor muestra que es posible para infinitos conjuntos tener cardinalities diferentes y en particular la cardinalidad del conjunto de números reales es mayor que la cardinalidad del conjunto de números naturales. También es posible para un subconjunto adecuado de un conjunto infinito que tienen la misma cardinalidad como el conjunto original, algo que no puede ocurrir con adecuada subconjuntos de finito establece.

Hay una secuencia de números cardinales transfinita:

$0, 1, 2, 3, \ldots, n, \ldots ; \aleph_0, \aleph_1, \aleph_2, \ldots, \aleph_{\alpha}, \ldots.\$

Esta secuencia se inicia con la números naturales incluyendo cero (cardenales finitos), que son seguidos por el números de Aleph (cardenales infinitas de conjuntos bien ordenados). Los números de aleph están indexados por números ordinales. Bajo el supuesto de la Axioma de la opción, esto secuencia Transfinito incluye todos los números cardinales. Si uno rechaza ese axioma, la situación es más complicada, con cardenales infinitos adicionales que no son alephs.

Cardinalidad es estudiado por su propio bien como parte de teoría de conjuntos. También es una herramienta utilizada en las ramas de las matemáticas, incluyendo combinatoria, álgebra abstracta, y Análisis matemático. En teoría de la categoría, la forma de números cardinales un esqueleto de la Categoría de conjuntos.

Historia

La noción de cardinalidad, según lo entendido ahora, fue formulada por Georg Cantor, el creador de teoría de conjuntos, en 1874 – 1884. Cardinalidad puede utilizarse para comparar un aspecto de conjuntos finitos; por ejemplo los conjuntos {1,2,3} y {4,5,6} no son igual, pero tienen el misma cardinalidad, es decir tres (esto se establece por la existencia de un biyección, es decir, una correspondencia uno a uno, entre los dos conjuntos; por ejemplo {1 -> 4, 2 -> 5, 3 -> 6}).

Cantor aplicó su concepto de biyección a conjuntos infinitos; por ejemplo el conjunto de los números naturales N = {0, 1, 2, 3, ...}. Por lo tanto, todos establece teniendo una biyección con N llamó conjuntos enumerables (infinitos contable) y todos tienen el mismo número cardinal. Se llama este número cardinal $\aleph_0$, Aleph-null. Llamó a los números cardinales de los conjuntos infinitos, números cardinales Transfinito.

Cantor demostrado que cualquier subconjunto ilimitada de N tiene la misma cardinalidad como N, aunque esto puede parecer ir en contra de intuición. También demostró que el conjunto de todos pares ordenados de los números naturales es enumerables (lo que implica que el conjunto de todos números racionales es enumerables) y más tarde demostró que el conjunto de todos números algebraicos también está lista. Cada número algebraico z puede ser codificado como una secuencia finita de enteros que son los coeficientes de la ecuación polinómica de la cual es la solución, es decir, la (n-tuplas ordenadasa₀, a₁, ..., a_n), a_i ∈ Z junto con un par de racionales (b₀, b₁) tal que z es la única raíz del polinomio con coeficientes (a₀, a₁, ..., a_n) que se encuentra en el intervalo (b₀, b₁).

En su papel de 1874, Cantor demostró que existen números de orden superior demostrando que el conjunto de números reales tiene cardinalidad mayor que la de N. Su presentación original utiliza una compleja discusión con intervalos anidados, pero en un papel de 1891 demostró el mismo resultado usando su ingenioso pero simple discusión diagonal. El nuevo número cardinal del conjunto de los números reales se llama el Cardinalidad del continuo y Cantor utiliza el símbolo $\mathfrak{c}$ para ello.

Cantor también desarrolló una gran parte de la teoría general de números cardinales; demostró que hay un menor número de cardinal Transfinito ($\aleph_0$aleph-null) y que por cada número cardinal, hay un cardenal mayor siguiente

$(\aleph_1, \aleph_2, \aleph_3, \cdots).\$

Su hipótesis del continuo es la propuesta que $\mathfrak{c}$ es la misma que $\aleph_1$. Esta hipótesis se ha encontrado para ser independiente de los axiomas estándar de teoría matemática; se puede probado ni refutado desde los supuestos estándar.

Motivación

En uso informal, un número cardinal es lo que normalmente se conoce como un número de cuenta, siempre que se incluye el 0: 0, 1, 2,... Ellos pueden ser identificados con el números naturales comenzando con 0. Los números de cuenta son exactamente lo que se puede definir formalmente como el finito números cardinales. Cardenales infinitos sólo ocurren en las matemáticas y lógica de más alto nivel.

Más formalmente, puede utilizarse un número distinto de cero para dos propósitos: para describir el tamaño de un conjunto, o para describir la posición de un elemento de una secuencia. Para los conjuntos finitos y secuencias es fácil ver que estas dos nociones coinciden, puesto que para cada número que describe una posición en una secuencia podemos construir un conjunto que tiene exactamente el tamaño correcto, por ejemplo 3 describe la posición de 'c' en la secuencia < 'a', 'b', 'c', lo ',... >, y podemos construir el conjunto {a, b, c} que tiene 3 elementos. Sin embargo cuando se trata con conjuntos infinitos es esencial distinguir entre los dos — las dos nociones de hecho son diferentes para conjuntos infinitos. Teniendo en cuenta la posición de aspecto conduce a números ordinales, mientras que el aspecto del tamaño es generalizado por la números cardinales se describe aquí.

La intuición detrás de la definición formal de Cardenal es la construcción de una noción del tamaño relativo o "grandeza" de un conjunto sin hacer referencia a la clase de miembros que tiene. Para conjuntos finitos es fácil; uno simplemente cuenta el número de elementos de que un conjunto. Para comparar los tamaños de los conjuntos más grandes, es necesario apelar a nociones más sutiles.

Un conjunto Y es al menos tan grande como un conjunto X Si hay un inyectiva Mapeo de los elementos de X a los elementos de Y. Una asignación inyectiva identifica cada elemento del conjunto X con un único elemento del conjunto Y. Esto es más fácil de entender por ejemplo; Supongamos que tenemos los conjuntos X = {1,2,3} y Y = {a, b, d, c}, entonces usando esta noción de tamaño observaríamos que existe una asignación:

1 → un

→ 2 b

3 → c

que es inyectiva y por lo tanto concluir que Y tiene cardinalidad mayor o igual a X. Tenga en cuenta el elemento d no tiene ninguna asignación de elemento a él, pero esto está permitido como sólo requieren una asignación inyectiva y no necesariamente un inyectiva y en mapeo. La ventaja de este concepto es que se puede extender a conjuntos infinitos.

Entonces podemos extender esto a una relación de igualdad-estilo. Dos establece X y Y se dice que tienen el mismo Cardinalidad Si existe un biyección entre X y Y. Por la Teorema de Schroeder – Bernstein, esto es equivalente a allí siendo ambos una asignación de inyectiva X Para Y y una asignación de inyectiva Y Para X. Escribimos entonces |X| = |Y|. El número cardinal de X se suele definirse como la menos ordinal a con |a| = |X|. Esto se llama el asignación de Cardenal von Neumann; para que esta definición a tener sentido, debe demostrarse que cada sistema tiene la misma cardinalidad como algunos ordinal; Esta declaración es la principio de ordenación bien. Es sin embargo posible para discutir la relativa cardinalidad de conjuntos sin explícitamente asignar nombres a los objetos.

El ejemplo clásico es el de la paradoja del hotel infinito, también llamada Paradoja de Hilbert del Grand Hotel. Supongo que eres un posadero en un hotel con un número infinito de habitaciones. El hotel está lleno, y luego llega un nuevo invitado. Es posible ajustar al huésped extra preguntándole el invitado que estaba en la sala 1 para pasar a la sala 2, el invitado en la sala 2 para pasar a la sala 3 y así sucesivamente, dejando espacio 1 vacante. Podemos escribir explícitamente un segmento de esta asignación:

1 ↔ 2

↔ 2 3

3 ↔ 4

...

n ↔ n + 1

...

De esta manera podemos ver que el conjunto {1,2,3,...} tiene la misma cardinalidad como el conjunto {2,3,4,...}, puesto que ha demostrado una biyección entre el primero y el segundo. Esto motiva la definición de un infinito establece que cualquier conjunto que tiene un subconjunto adecuado de la misma cardinalidad; en este caso {2,3,4,...} es un subconjunto apropiado de {1,2,3,...}.

Al considerar estos objetos grandes, también querríamos ver si la noción de contar orden coincide con la del cardenal definido anteriormente para estas series infinitas. Sucede que no; teniendo en cuenta el ejemplo anterior que podemos ver que si existe algún objeto "uno mayor de infinito", entonces debe tener la misma cardinalidad como el conjunto infinito empezamos con. Es posible utilizar una noción formal diferente número, llamado números ordinales, basado en las ideas del conteo y teniendo en cuenta cada número a su vez, y descubrimos que las nociones de cardinalidad y ordinality son divergentes, una vez que pasamos de los números finitos.

Se puede probar que la cardinalidad de la números reales es mayor que el de los números naturales que acabo de describir. Esto puede visualizarse mediante Discusión diagonal de cantor; preguntas clásicas de cardinalidad (por ejemplo el hipótesis del continuo) se refieren a descubrir si existe algún cardenal entre un par de otros cardenales infinitos. En tiempos más recientes los matemáticos han estado describiendo las propiedades de los cardenales más grandes.

Cardinalidad es un concepto tan común en matemáticas, una variedad de nombres están en uso. Uniformidad de cardinalidad se refiere a veces como equipotence, equipollence, o equinumerosity. Así se dice que dos conjuntos con la misma cardinalidad son, respectivamente, equipotente, equiparables, o equinumerous.

Definición formal

Formalmente, asumiendo la Axioma de la opción, la cardinalidad de un conjunto X es el menos ordinal α tal que existe una biyección entre X y α. Esta definición es conocida como la asignación de Cardenal von Neumann. Si no se asume el axioma de la opción que necesitamos hacer algo diferente. La definición más antigua de la cardinalidad de un conjunto X (en Cantor implícitos y explícitos en Frege y Principia Mathematica) es como la clase [X] de todos los conjuntos que son equinumerous con X. Esto no funciona ZFC u otros relacionados con sistemas de teoría determinada axiomática Porque si X es no-vacío, esta colección es demasiado grande para ser un conjunto. De hecho, para X ≠ ∅ Hay una inyección del universo en [X] mediante la asignación de un conjunto m Para {m} × X y así por el Axioma de la limitación de tamaño, [X] es una clase apropiada. La definición funciona sin embargo en Mecanografíe la teoría y en Nuevas fundaciones y sistemas relacionados. Sin embargo, si restringimos de esta clase a esos equinumerous con X tienen menos Rank, entonces va a funcionar (este es un truco debido a Dana Scott: funciona porque la colección de objetos con cualquier rango determinado es un conjunto).

Formalmente, el orden entre números cardinales se define de la siguiente manera: |X| ≤ |Y| significa que existe un inyectiva función de X Para Y. El Teorema de cantor – Bernstein – Schroeder Eso si los Estados |X| ≤ |Y| y |Y| ≤ |X| Entonces |X| = |Y|. El Axioma de la opción es equivalente a la declaración que dio dos conjuntos X y Y, tampoco |X| ≤ |Y| o |Y| ≤ |X|.

Un conjunto X es Dedekind-infinito Si existe un subconjunto adecuado Y de X con |X| = |Y|, y Dedekind-finita Si no existe tal un subconjunto. El finito cardenales son sólo el números naturales, es decir, un conjunto X es finito si y sólo si |X| = |n| = n para un número natural n. Cualquier otro conjunto es infinito. Suponiendo que el axioma de la opción, puede probarse que las nociones de Dedekind corresponden al estándar. 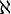Se puede también ser demostrado que el cardenal $\aleph_0$ (Aleph nulo o aleph-0, donde aleph es la primera letra en el Alfabeto hebreo, representado $\aleph$) del conjunto de los números naturales es el cardenal infinito más pequeño, es decir, que cualquier conjunto infinito tiene un subconjunto de cardinalidad $\aleph_0.$ El cardenal más grande siguiente se denota por $\aleph_1$ y así sucesivamente. Para todos los ordinal Allí α es un número cardinal $\aleph_{\alpha},$ y esta lista agota todos los números cardinales infinitos.

Cardenal aritmética

Podemos definir aritmética operaciones en números cardinales que generalizan las operaciones ordinarias para los números naturales. Puede ser demostrado que para cardenales finitos estas operaciones coinciden con las operaciones habituales para los números naturales. Además, estas operaciones comparten muchas características con la aritmética ordinaria.

Cardenal sucesor

Para más detalles sobre este tema, ver Cardenal sucesor.

Si se mantiene el axioma de la opción, cada cardenal κ tiene un sucesor κ⁺ > Κ, y no sin cardenales entre κ y su sucesor. Para cardenales finitos, el sucesor es simplemente κ + 1. Para cardenales infinitas, el cardenal sucesor difiere de la ordinal sucesor.

Además de cardenal

If X y Y son disjuntos, además está dada por la Unión de X y Y. Si los dos conjuntos son no ya separados, entonces puede reemplazarse por conjuntos disjuntos de la misma cardinalidad, por ejemplo, reemplazar X por X× {0} y Y por Y×{1}.

$|X| + |Y| = | X \cup Y|.$

Cero es una identidad aditiva κ + 0 = 0 + κ = κ.

Además es asociativa (κ + μ) + ν = κ + (μ + ν).

Además es conmutativa κ + μ = μ + κ.

Además es no decreciente en dos argumentos:

$(\kappa \le \mu) \rightarrow ((\kappa + \nu \le \mu + \nu) \mbox{ and } (\nu + \kappa \le \nu + \mu)).$

Suponiendo que el axioma de la opción, es fácil adición de números cardinales infinitos. Si κ o μ es infinita, entonces

$\kappa + \mu = \max\{\kappa, \mu\}\,.$

Resta

Suponiendo que el axioma de elección y, teniendo en cuenta un σ cardinal infinito y un cardenal μ, existe un cardenal κ tal que μ + κ = σ si y sólo si σ ≤ μ. Será única (e igual a σ) si y solamente si μ < σ.

Cardenal multiplicación

El producto de los cardenales proviene de la producto cartesiano.

$|X|\cdot|Y| = |X \times Y|$

κ·0 = 0·κ = 0.

κ·μ = 0 → (κ = 0 o μ = 0).

Uno es una identidad multiplicativa κ·1 = 1·κ = κ.

La multiplicación es asociativa)κ·μ)·ν = κ·(μ·ν).

La multiplicación es conmutativa κ·μ = μ·κ.

La multiplicación es no decreciente en dos argumentos: κ ≤ μ → (κ·ν ≤ μ·ν y ν·κ ≤ ν·μ).

Multiplicación distribuye en adición: κ·(μ + ν) = κ·μ + κ·ν y)μ + ν)·κ = μ·κ + ν·κ.

Suponiendo que el axioma de la opción, la multiplicación de números cardinales infinitos también es fácil. Si cualquiera κ o μ es infinito y ambos son cero, entonces

$\kappa\cdot\mu = \max\{\kappa, \mu\}.$

División

Suponiendo que el axioma de elección y, dado un cardinal infinito π y un μ cardinal distinto de cero, existe un cardenal κ tal que μ · Κ = π Si y sólo si ≤ μ π. Será única (e igual a π) si y solamente si μ < π.

Exponenciación cardinal

Exponenciación es dada por

$|X|^{|Y|} = \left|X^Y\right|$

donde X^Y es el conjunto de todos funciones De Y Para X.

κ ⁰ = 1 (en particular 0 ⁰ = 1), ver función vacía.

Si 1 ≤ μ, entonces 0 ^μ = 0.

1 ^μ = 1.

κ ¹ = Κ.

κ ^{Μ + Ν} = κ ^μ· κ ^ν.

κ ^{Μ · Ν} = ( κ ^μ) ^ν.

( κ· μ) ^ν = κ ^ν· μ ^ν.

Exponenciación es no decreciente en dos argumentos:

(1 ≤ ν y κ ≤ μ) → ( ν ^κ ≤ ν ^μ) y

( κ ≤ μ) → ( κ ^ν ≤ μ ^ν).

Tenga en cuenta que 2^|X| es la cardinalidad de la conjunto potencia del conjunto de X y Discusión diagonal de cantor muestra que 2^|X| > |X| para cualquier conjunto X. Esto demuestra que no existe ningún cardenal mayor (porque para cualquier cardenal κ, siempre podemos encontrar un cardenal mayor 2^κ). De hecho, la clase de los cardenales es un clase apropiada. (Esta prueba falla en algunas teorías de conjunto, en particular Nuevas fundaciones.)

El axioma de la opción asumen que todas las proposiciones restantes en esta sección:

If κ y μ son finitos y mayor que 1, y ν es infinita, entonces κ ^ν = μ ^ν.

If κ es infinito y μ es finito y distinto de cero, entonces κ ^μ = κ.

Si 2 κ ≤ y 1 ≤ μ y al menos uno de ellos es infinita, entonces:

Max (κ, 2 ^μ) ≤ κ ^μ ≤ Max (2 ^κ2 ^μ).

Usando Teorema de Königuno puede probar κ < κ^CF(κ) y κ < cf (2^κ) para cualquier κ cardinal infinito, donde cf(κ) es el Cofinalidad de κ.

Raíces

Suponiendo que el axioma de elección y, teniendo en cuenta un κ cardinal infinito y un μ cardinal finito mayor que 0, el cardenal ν satisfactoria ${\nu}^{\mu}={\kappa}$ será κ.

Logaritmos

Suponiendo que el axioma de elección y, teniendo en cuenta un κ cardinal infinito y un μ cardinal finito mayor que 1, puede o no ser un cardenal λ satisfactorio ${\mu}^{\lambda}={\kappa}$. Sin embargo, si existe tal un cardenal, es infinito y menos que κ y cualquier ν cardinalidad finita mayor que 1 también satisfará 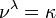${\nu}^{\lambda}={\kappa}$.

El logaritmo de un número cardinal infinito κ se define como el menos μ número cardinal tal que κ ≤ 2^μ. Los logaritmos de los cardenales infinitos son útiles en algunos campos de las matemáticas, por ejemplo en el estudio del cardenal invariantes de espacios topológicos, aunque carecen de algunas de las propiedades que poseen los logaritmos de números verdaderos positivos.

La hipótesis del continuo

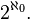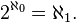El hipótesis del continuo (CH) afirma que hay no hay cardenales estrictamente entre $\aleph_0$ y $2^{\aleph_0}.$ El último número cardinal también a menudo se denota por $\mathfrak{c}$; es el Cardinalidad del continuo (el conjunto de números reales). En este caso $2^{\aleph_0} = \aleph_1.$ El hipótesis del continuo generalizado (GCH) establece que para cada conjunto infinito X, no hay cardenales estrictamente entre |X| y 2^|X|. La hipótesis del continuo es independiente de los axiomas habituales de teoría de conjuntos, los axiomas de Zermelo-Fraenkel junto con el axioma de elección (ZFC).

Véase también

• Contando
• Nombres de los números en inglés
• Gran cardenal
• Principio de inclusión-exclusión

• Número nominal
• Número ordinal
• Cardenal regular

• La paradoja del cardenal mayor
• Número de Aleph
• Número de Beth

Referencias

Notas

Bibliografía

• Dauben, Joseph Warren (1990), Georg Cantor: Sus matemáticas y filosofía del infinitoPrinceton: Princeton University Press, ISBN0691-02447-2
• Hahn, Hans, InfinitoParte IX, capítulo 2, volumen 3 de El mundo de las matemáticas. Nueva York: Simon and Schuster, 1956.
• Halmos, Paul, Teoría determinada ingenua. Princeton, NJ: D. Van Nostrand Company, 1960. Reimpreso por Springer-Verlag, Nueva York, 1974. ISBN 0-387-90092-6 (Edición de springer-Verlag).

Enlaces externos

• Hazewinkel, Michiel, ed. (2001), "Número Cardinal", Enciclopedia de las matemáticas, Springer, ISBN978-1-55608-010-4
• Weisstein, Eric W., "Número Cardinal", MathWorld.
• Cardinalidad en ProvenMath pruebas de los teoremas básicos de cardinalidad.

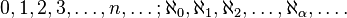
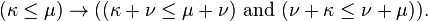
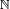Otras Páginas

• Ed Fagan (abogados de categoria Disbarred)
• Estado y la Asociacion de directores de prevencion de lesiones Territorial
• Instituto de terapia en linea
• Lista de hospitales en Estonia
• MindSpring (categoria Internet los proveedores de servicios de los Estados Unidos)
• Coincidencia de patron comprimido