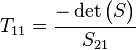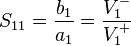Parámetros de dispersión
Parámetros de dispersión o S-parámetros (los elementos de un matriz de dispersión o S-matriz) describir el comportamiento eléctrico de lineal redes eléctricas Cuando sometidos a varios estado estacionario estímulos por señales eléctricas.
Los parámetros son útiles para Ingeniería eléctrica, Ingeniería electrónica, y sistemas de comunicación diseño y especialmente para Ingeniería de microondas.
Los parámetros de S son miembros de una familia de parámetros similares, otros ejemplos están: Y parámetros,[1] Z-parámetros,[2] H-parámetros, T-parámetros o ABCD-parámetros.[3][4] Se diferencian de éstos, en el sentido que S-parámetros No utilice abierto o condiciones de corto circuito para caracterizar una red eléctrica lineal; en cambio, cargas combinadas se utilizan. Estos terminaciones son más fáciles de utilizar en frecuencias de la señal alta de circuito abierto y terminaciones de cortocircuito. Además, las cantidades se miden en términos de poder.
Muchas propiedades eléctricas de las redes de componentes (inductores, condensadores, resistencias) puede expresarse utilizando S-parámetros, tales como ganancia, pérdida de retorno, relación de ondas estacionarias de voltaje (ROE), coeficiente de reflexión y amplificador estabilidad. El término 'dispersión' es más común Ingeniería óptica de ingeniería de RF, refiriéndose al efecto observado cuando un plano de la onda electromagnética es incidente en una obstrucción o pasa a través de diferentes dieléctrico medios de comunicación. En el contexto de parámetros S, dispersión se refiere a la forma en que los viajes corrientes y voltajes en un línea de transmisión se ven afectados cuando cumplen una discontinuidad causada por la inserción de una red en la línea de transmisión. Esto es equivalente a la reunión de onda un impedancia a diferencia de la línea Impedancia característica.
Aunque aplicable en cualquier frecuenciaS-parámetros se utilizan principalmente para redes que operan en frecuencia de radio (RF) y microondas frecuencias donde las consideraciones de potencia y energía de señal son más fácilmente cuantificables de tensiones y corrientes. S-parámetros cambian con la frecuencia de medición, para frecuencia debe especificarse para cualquier medición de parámetros S indicado, además de la Impedancia característica o impedancia del sistema.
S-parámetros fácilmente están representados en matriz forma y obedecer las reglas del álgebra matricial.
Contenido
- 1 Fondo
- 2 El general S-parámetro matrix
- 2.1 Definición
- 2.2 Reciprocidad
- 2.3 Redes Lossless
- 2.4 Redes con pérdida
- 3 Dos puertos S-parámetros
- 4 Parámetro S propiedades de redes de 2 puertos
- 4.1 Complejo aumento lineal
- 4.2 Aumento lineal escalar
- 4.3 Ganancia logarítmica escalar
- 4.4 Pérdida de inserción
- 4.5 Pérdida de retorno de entrada
- 4.6 Pérdida de retorno de salida
- 4.7 Ganancia inversa y aislamiento inverso
- 4.8 Coeficiente de reflexión del voltaje
- 4.9 Relación de ondas estacionarias de voltaje
- 5 4 puertos S-parámetros
- 5.1 Modo mixto S-parámetros de 4 puertos
- 6 S-parámetros en el diseño de amplificador
- 6.1 Puerto de carga las condiciones para un amplificador para ser incondicionalmente estable
- 6.1.1 valores de (círculo de estabilidad de salida)
- 6.1.2 valores de (círculo de estabilidad entrada)
- 6.2 Parámetros de dispersión transferencia
- 6.1 Puerto de carga las condiciones para un amplificador para ser incondicionalmente estable
- 7 S-parámetros de 1 puerto
- 8 Matrices de S-parámetro de orden superior
- 9 Medición de parámetros de S
- 9.1 Analizador de redes vectoriales
- 9.2 Calibración
- 9.3 Minimización de errores sistemáticos
- 9.4 Formato de salida de datos S-parámetro medidos y corregidos
- 9.5 Formato de lista
- 9.6 Gráfico (carta de Smith)
- 9.7 Gráfico (Diagrama polar)
- 9.8 Medición de parámetros de S de una red de un puerto
- 9.9 S-parámetros de medición de redes con más de 2 puertos
- 10 Véase también
- 11 Referencias
- 12 Bibliografía
Fondo
Fue la primera descripción publicada de S-parámetros en la tesis de Vitold Belevitch en 1945.[5] Era el nombre usado por Belevitch matriz de repartición y consideración limitada a las redes de elementos agrupados. El término matriz de dispersión fue utilizado por el físico e ingeniero Robert Henry Dicke en 1947 que desarrolló independientemente la idea durante el trabajo de la guerra en el radar.[6][7] La técnica fue popularizada en la década de 1960 por Kaneyuka Kurokawa[8]
En el enfoque del parámetro-S, la red eléctrica es considerada como un 'caja negra' que contiene varios interconectados los componentes del circuito eléctrico básico o agrupan elementos como resistencias, condensadores, bobinas y transistores, que interactúa con otros circuitos a través de puertos. La red se caracteriza por una plaza matriz de números complejos llama su matriz del parámetro S, que puede utilizarse para calcular su respuesta a las señales aplicadas a los puertos.
Para la definición del parámetro-S, se entiende que una red puede contener cualquiera de los componentes siempre que comporta toda la red linealmente con señales de pequeñas incidentes. También puede incluir muchos componentes del sistema de comunicación típica o 'bloques' tales como Amplificadores, atenuadores, filtros, acopladores y Ecualizadores proporciona también operan bajo condiciones definidas y lineales.
La red eléctrica a ser descrito por parámetros de S puede tener cualquier número de puertos. Los puertos son los puntos en que las señales eléctricas o entrar o salir de la red. Los puertos son generalmente los pares de terminales con el requisito de que el actual en un terminal es igual a la corriente dejando a la otra.[9][10] S-parámetros se utilizan en las frecuencias donde suelen ser los puertos coaxial o Guía de onda conexiones.
El parámetro-S matriz describiendo un N-red de Puerto será cuadrada de dimensión N y por lo tanto, contendrá  elementos. En la frecuencia de prueba cada elemento o parámetro-S está representada por una sin unidades número complejo Eso representa magnitud y ángulo, es decir, amplitud y fase. Tampoco se puede expresar el número complejo en rectangular forma o, más comúnmente, en polar formulario. La magnitud del parámetro S puede expresarse en forma lineal o forma logarítmica. Cuando se expresa en forma logarítmica, magnitud tiene el "unidad adimensional"de decibelios. El ángulo S-parámetro se expresa con mayor frecuencia en grados Pero de vez en cuando, en radianes. Cualquier parámetro S puede visualizarse gráficamente en un diagrama polar de un punto para una frecuencia o un lugar geométrico para un rango de frecuencias. Si se aplica a un puerto único (siendo de la forma
elementos. En la frecuencia de prueba cada elemento o parámetro-S está representada por una sin unidades número complejo Eso representa magnitud y ángulo, es decir, amplitud y fase. Tampoco se puede expresar el número complejo en rectangular forma o, más comúnmente, en polar formulario. La magnitud del parámetro S puede expresarse en forma lineal o forma logarítmica. Cuando se expresa en forma logarítmica, magnitud tiene el "unidad adimensional"de decibelios. El ángulo S-parámetro se expresa con mayor frecuencia en grados Pero de vez en cuando, en radianes. Cualquier parámetro S puede visualizarse gráficamente en un diagrama polar de un punto para una frecuencia o un lugar geométrico para un rango de frecuencias. Si se aplica a un puerto único (siendo de la forma 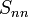 ), puede mostrarse en una impedancia o admitancia Carta de Smith normalizada a la impedancia del sistema. La carta de Smith permite conversión simple entre el
), puede mostrarse en una impedancia o admitancia Carta de Smith normalizada a la impedancia del sistema. La carta de Smith permite conversión simple entre el 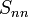 parámetro, equivalente a los asociados y el coeficiente de reflexión del voltaje (normalizada) Impedancia (o entrada) 'visto' en ese puerto.
parámetro, equivalente a los asociados y el coeficiente de reflexión del voltaje (normalizada) Impedancia (o entrada) 'visto' en ese puerto.
Cuando se especifica un conjunto de parámetros de S se debe definir la siguiente información:
- La frecuencia de
- La impedancia característica (a menudo 50 Ω)
- La asignación de números de Puerto
- Condiciones que puedan afectar a la red, tales como temperatura, controlan de tensión y polarización actuales, en su caso.
El general S-parámetro matrix
Definición
Para una red multipuerto genérica, los puertos están numerados de 1 a N, donde N es el número total de puertos. Para el puerto n, la definición de parámetro S asociada es en términos de incidente y refleja 'olas de energía',  y
y  respectivamente.
respectivamente.
Kurokawa[11] define la onda incidente energía para cada puerto como
y la onda reflejada para cada puerto se define como
donde  es la matriz diagonal de la impedancia compleja de referencia para cada puerto,
es la matriz diagonal de la impedancia compleja de referencia para cada puerto,  es el conjugado complejo elementwise de
es el conjugado complejo elementwise de  ,
,  y
y  son respectivamente los vectores de la columna de las tensiones y corrientes en cada puerto y
son respectivamente los vectores de la columna de las tensiones y corrientes en cada puerto y
A veces es útil asumir que la impedancia de referencia es el mismo para todos los puertos en cuyo caso pueden simplificarse las definiciones de las ondas incidentes y reflejadas a
y
Para todos los puertos de las ondas de potencia reflejada pueden definirse en términos de la matriz del parámetro-S y las ondas de energía incidente mediante la siguiente ecuación de matriz:
donde S es una N x N matriz de los elementos de los cuales pueden ser indexados usando convencional matriz (matemáticas) notación.
Reciprocidad
Será una red recíproco Si es pasivo y contiene solamente de recíprocos materiales que influyen en la señal transmitida. Por ejemplo, atenuadores, cables, divisores y combinadores son redes todo recíprocas y  en cada caso, o el parámetro-S matriz será igual a su transponer. Redes que incluyen materiales no-recíproco en el medio de transmisión como los que contienen magnéticamente parcial ferrita componentes serán no recíproco. Un amplificador es otro ejemplo de una red sin reciprocidad.
en cada caso, o el parámetro-S matriz será igual a su transponer. Redes que incluyen materiales no-recíproco en el medio de transmisión como los que contienen magnéticamente parcial ferrita componentes serán no recíproco. Un amplificador es otro ejemplo de una red sin reciprocidad.
Una propiedad interesante de las redes de 3 puertos, sin embargo, es que no puede ser simultáneamente recíproco, pérdida-libre y perfectamente emparejado.[12]
Redes Lossless
Una red sin pérdidas es uno que no disipan energía, o:  . La suma de las potencias incidentes en todos los puertos es igual a la suma de las potencias se refleja en todos los puertos. Esto implica que la matriz del parámetro-S unitarioEs decir
. La suma de las potencias incidentes en todos los puertos es igual a la suma de las potencias se refleja en todos los puertos. Esto implica que la matriz del parámetro-S unitarioEs decir  , donde
, donde  es el transpuesta conjugada de
es el transpuesta conjugada de  y
y  es el matriz identidad.
es el matriz identidad.
Redes con pérdida
A lossy Red pasiva es uno en el que la suma de las potencias incidentes en todos los puertos es mayor que la suma de las potencias se refleja en todos los puertos. Por lo tanto disipa energía, o:  . En este caso
. En este caso  , y
, y 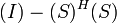 es definida positiva.
es definida positiva.
Dos puertos S-parámetros

La matriz del parámetro-S para la red de 2 puertos es probablemente el más comúnmente usado y sirve como el elemento básico para la generación de las matrices de orden superiores para redes más grandes.[13] En este caso la relación entre las ondas de energía incidente, reflejada y la matriz de parámetros S está dada por:
-
 .
.
Ampliando las matrices en ecuaciones da:
y
-
 .
.
Cada ecuación da la relación entre las ondas de energía incidente y reflejada en cada uno de la red de puertos, 1 y 2, en términos de S-parámetros individuales de la red,  ,
,  ,
, 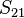 y
y  . Si uno considera que una onda de energía incidente en (puerto 1
. Si uno considera que una onda de energía incidente en (puerto 1 ) que puede resultar desde ondas saliendo desde Puerto 1 sí mismo ()
) que puede resultar desde ondas saliendo desde Puerto 1 sí mismo () ) o (puerto 2)
) o (puerto 2) ). Sin embargo, si, de acuerdo a la definición de parámetros de S, puerto 2 se termina en una idéntica a la (impedancia) sistema de carga
). Sin embargo, si, de acuerdo a la definición de parámetros de S, puerto 2 se termina en una idéntica a la (impedancia) sistema de carga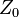 ) entonces, por el Teorema de la transferencia de potencia máxima,
) entonces, por el Teorema de la transferencia de potencia máxima,  será totalmente absorto haciendo
será totalmente absorto haciendo  igual a cero. Por lo tanto, definir las ondas de voltaje incidente como
igual a cero. Por lo tanto, definir las ondas de voltaje incidente como  y
y  con la reflejada olas ser
con la reflejada olas ser  y
y  ,
,
-
 y
y
 .
.
De manera similar, si termina en la impedancia del sistema entonces puerto 1  llega a ser cero, dando
llega a ser cero, dando
-
 y
y

Cada parámetro 2 puertos-S tiene las siguientes descripciones genéricas:
-
 es el coeficiente de reflexión de Puerto de entrada voltaje
es el coeficiente de reflexión de Puerto de entrada voltaje
-
 es la ganancia de voltaje inverso
es la ganancia de voltaje inverso
-
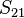 es la ganancia de tensión
es la ganancia de tensión
-
 es el coeficiente de reflexión del voltaje salida puerto.
es el coeficiente de reflexión del voltaje salida puerto.
Si, en lugar de definir la dirección de onda de voltaje con respecto a cada puerto, son definidos por su dirección absoluta como adelante  y marcha atrás
y marcha atrás  Entonces las ondas
Entonces las ondas 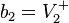 y
y 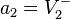 . Los parámetros S tome un significado más intuitiva, tales como la tensión de paso ganar se define por el cociente de la tensión hacia adelante
. Los parámetros S tome un significado más intuitiva, tales como la tensión de paso ganar se define por el cociente de la tensión hacia adelante  .
.
Parámetro S propiedades de redes de 2 puertos
Un amplificador operando bajo condiciones lineales (pequeña señal) es un buen ejemplo de una red sin reciprocidad y un atenuador emparejado es un ejemplo de una red recíproca. En los siguientes casos que asumimos que las conexiones de entrada y salidas son a los puertos 1 y 2 respectivamente, que es la Convención más comunes. La impedancia nominal del sistema, frecuencia y otros factores que pueden influir sobre el dispositivo, como la temperatura, también deben especificarse.
Complejo aumento lineal
El aumento lineal complejo G está dada por
-
 .
.
Es simplemente la ganancia de voltaje como una relación lineal de la tensión de salida dividida por la tensión de entrada, todos los valores expresados en cantidades complejas.
Aumento lineal escalar
La ganancia lineal escalar (o magnitud de aumento lineal) está dada por
-
 .
.
Es simplemente la ganancia de voltaje escalares como una relación lineal de la tensión de salida y el voltaje de entrada. Como esto es una cantidad escalar, la fase no es relevante en este caso.
Ganancia logarítmica escalar
Las escalar expresión logarítmica (decibelio o dB) para ganancia (g) es
-
 dB.
dB.
Esto es más comúnmente utilizado que escalar ganancia lineal y una cantidad positiva normalmente se entiende como simplemente una 'ganancia'... Una cantidad negativa puede expresarse como una ganancia' negativa', o más generalmente como una 'pérdida' equivalente a su magnitud en dB. Por ejemplo, una longitud de 10 m de cable puede tener una ganancia de - 1 dB a 100 MHz o una pérdida de 1 dB a 100 MHz.
Pérdida de inserción
En la medida de los casos los dos puertos utilizan la misma impedancia de referencia, el (pérdida de inserciónIL) es la magnitud del coeficiente de transmisión |S21| expresado en decibelios. Por lo tanto es dado por:[14]
 dB.
dB.
Es la pérdida adicional producida por la introducción de la dispositivo bajo prueba (DUT) entre los 2 planos de referencia de la medición. Tenga en cuenta que la pérdida adicional puede introducirse por pérdida intrínseca en el DUT o desajuste. En caso de pérdida adicional la pérdida de inserción se define como positivo. La negativa de la pérdida de inserción, expresada en decibelios se define como ganancia de inserción.
Pérdida de retorno de entrada
Entrada pérdida de retorno (RLin) puede ser pensado como una medida de cuán cerca la impedancia real de entrada de la red es el valor de la impedancia nominal del sistema. Pérdida de retorno entrada expresada en decibelios está dada por
-
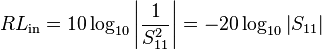 dB.
dB.
Tenga en cuenta que para las redes de dos puertos pasivas en la cual |S11| ≤ 1, se sigue que la pérdida de retorno es una cantidad no negativo: RLin≥ 0. También tenga en cuenta que alguna manera confusa, pérdida de retorno se utiliza a veces como el negativo de la cantidad definida anteriormente, pero en sentido estricto, este uso es incorrecto basado en la definición de pérdida.[15]
Pérdida de retorno de salida
La pérdida de retorno () salidaRLhacia fuera) tiene una definición similar a la pérdida de retorno de entrada pero se aplica al salida Puerto (2) en lugar del puerto de entrada. Es dada por
-
 dB.
dB.
Ganancia inversa y aislamiento inverso
Las escalar expresión logarítmica (decibelio o dB) para ganancia inversa ( ) es:
) es:
-
 dB.
dB.
A menudo esto se expresará como aislamiento inversa)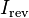 ) en cuyo caso se convierte en una cantidad positiva igual a la magnitud de
) en cuyo caso se convierte en una cantidad positiva igual a la magnitud de  y la expresión se convierte en:
y la expresión se convierte en:
-
 dB.
dB.
Coeficiente de reflexión del voltaje
El coeficiente de reflexión del voltaje en el puerto de entrada ( ) o en el (puerto de salida
) o en el (puerto de salida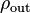 ) son equivalentes a
) son equivalentes a  y
y  respectivamente, entonces
respectivamente, entonces
-
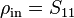 y
y
 .
.
Como  y
y  son cantidades complejas, tan
son cantidades complejas, tan  y
y 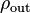 .
.
Los coeficientes de reflexión de voltaje son cantidades complejas y pueden representarse gráficamente en diagramas polares o cartas de Smith
Véase también el Coeficiente de reflexión artículo.
Relación de ondas estacionarias de voltaje
La relación de ondas estacionarias de voltaje (ROE) en un puerto, representada por la minúscula ', es una medida similar del partido puerto a pérdida de retorno, pero es una cantidad escalar lineal, el cociente de la tensión máxima de onda a la tensión mínima de ondas estacionarias. Por lo tanto se refiere a la magnitud del coeficiente de reflexión voltaje y por ende a la magnitud de cualquiera de los  para el puerto de entrada o
para el puerto de entrada o  para el puerto de salida.
para el puerto de salida.
En el puerto de entrada, el (VSWR ) está dada por
) está dada por
En el puerto de salida, el (VSWR ) está dada por
) está dada por
Esto es correcto para los coeficientes de reflexión de una magnitud no mayor que la unidad, que suele ser el caso. Un coeficiente de reflexión con una magnitud mayor que la unidad, tales como en un amplificador de diodo túnel, resultará en un valor negativo para esta expresión. VSWR, sin embargo, desde su definición, es siempre positivo. Una expresión más correcta para el puerto k de un multipuerto es;
4 puertos S-parámetros
4 parámetros del puerto de S son utilizados para caracterizar las redes puerto 4. Incluyen información sobre las olas de energía incidente y reflejada entre los 4 puertos de la red.
Comúnmente se utilizan para analizar un par de líneas de transmisión acoplados para determinar la cantidad de diafonía entre ellos, si ellos son impulsados por dos señales terminadas solas independientes, o la energía incidente y reflejada de señal diferencial impulsada a través de ellos. Muchas especificaciones de señales diferenciales de alta velocidad de definen un canal de comunicación en cuanto a la S 4-Port-parámetros, por ejemplo la interfaz de la unidad de 10 gigabits accesorio (XAUI), SATA, PCI-X y sistemas de InfiniBand.
Modo mixto S-parámetros de 4 puertos
4-Puerto Multimodal S-parámetros caracterizan una red 4 puertos en términos de la respuesta de la red a las señales comunes de estímulo modo y diferencial. La siguiente tabla muestra la mezcla 4-Port-modo S-parámetros.
| Estímulo | ||||||
|---|---|---|---|---|---|---|
| Diferencial | Modo común | |||||
| Puerto 1 | Puerto 2 | Puerto 1 | Puerto 2 | |||
| Respuesta | Diferencial | Puerto 1 | SDD11 | SDD12 | SDC11 | SDC12 |
| Puerto 2 | SDD21 | SDD22 | SDC21 | SDC22 | ||
| Modo común | Puerto 1 | SCD11 | SCD12 | SCC11 | SCC12 | |
| Puerto 2 | SCD21 | SCD22 | SCC21 | SCC22 | ||
Tenga en cuenta el formato de la notación del parámetro SXYab, donde "S" está parado para el parámetro de dispersión o S, "X" es el modo de respuesta (diferencial o común), "Y" es el modo de estímulo (diferencial o común), "a" es el puerto de respuesta (salida) y b es el puerto de estímulo (entrada). Esta es la nomenclatura típica para parámetros de dispersión.
El primer cuadrante se define como la superior izquierda 4 parámetros que describen el estímulo diferencial y las características de respuesta diferencial del dispositivo bajo prueba. Este es el modo actual de funcionamiento para diferencial de más alta velocidad interconecta y es el cuadrante que recibe la mayor atención. Incluye pérdida de inserción diferencial de entrada pérdida diferencial de retorno (SDD11), entrada (SDD21), salida diferencial devolver la pérdida (SDD22) y pérdida de inserción diferencial (SDD12) de salida. Son algunos de los beneficios del proceso de señal diferencial;
- reduce la susceptibilidad de interferencia electromagnética
- reducción de la radiación electromagnética del circuito diferencial equilibrado
- incluso productos de distorsión diferencial la orden transformados a las señales de modo común
- factor de dos aumento de nivel de tensión en relación con balanceado
- rechazo a tierra ruido codificación señal diferencial y suministro de modo común
Los cuadrantes de segundo y terceros son la parte superior derecha e inferior izquierdos 4 parámetros, respectivamente. Estos también se conocen como los cuadrantes de modo transversal. Esto es porque caracterizan completamente cualquier conversión de modo que ocurren en el dispositivo bajo prueba, si es la conversión de SDCab común-a-diferencial (susceptibilidad EMI para una señal diferencial prevista aplicación transmisión SDD) o diferencial-a-common SCDab conversión (radiación EMI para una aplicación diferenciada). Conversión de modo de comprensión es muy útil cuando tratando de optimizar el diseño de las interconexiones para transferencia de datos gigabit.
El cuarto cuadrante es los bajos parámetros de derecho 4 y describe las características de rendimiento de la señal de modo común SCCab propagar a través del dispositivo bajo prueba. Para un dispositivo diferencial SDDab correctamente diseñado debe haber mínimo común-modo de salida SCCab. Sin embargo, los datos de respuesta común-modo cuadrante IV es una medida de respuesta común-modo transmisión y utilizan en una relación con la respuesta de transmisión diferencial para determinar el rechazo de modo común de red. Este rechazo de modo común es un beneficio importante de procesamiento de señal diferencial y puede reducirse a uno en algunas implementaciones de circuito diferencial.[16][17]
S-parámetros en el diseño de amplificador
El parámetro de aislamiento inverso  determina el nivel de retroalimentación de la salida de un amplificador a la entrada y por lo tanto influye su estabilidad (su tendencia a abstenerse de oscilación) junto con la ganancia hacia adelante
determina el nivel de retroalimentación de la salida de un amplificador a la entrada y por lo tanto influye su estabilidad (su tendencia a abstenerse de oscilación) junto con la ganancia hacia adelante 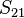 . Un amplificador con entrada y puertos de salida perfectamente aislados entre sí tendría registro escalares infinita magnitud aislamiento o la magnitud lineal de
. Un amplificador con entrada y puertos de salida perfectamente aislados entre sí tendría registro escalares infinita magnitud aislamiento o la magnitud lineal de  sería cero. Tan un amplificador se dice que es unilateral. Los amplificadores más prácticos aunque tendrá un aislamiento finito permitiendo que el coeficiente de reflexión 'visto' en la entrada para ser influenciado en cierta medida por la carga conectada a la salida. Un amplificador que deliberadamente está diseñado para tener el menor valor posible de
sería cero. Tan un amplificador se dice que es unilateral. Los amplificadores más prácticos aunque tendrá un aislamiento finito permitiendo que el coeficiente de reflexión 'visto' en la entrada para ser influenciado en cierta medida por la carga conectada a la salida. Un amplificador que deliberadamente está diseñado para tener el menor valor posible de  a menudo se llama un buffer amplificador.
a menudo se llama un buffer amplificador.
Supongamos que el puerto de salida de un real (no-unilateral o bilateral) amplificador está conectado a una carga arbitraria con un coeficiente de reflexión de  . El coeficiente de reflexión real 'visto' en el puerto de entrada
. El coeficiente de reflexión real 'visto' en el puerto de entrada  se dará por[18]
se dará por[18]
-
 .
.
Si el amplificador es unilateral y  y
y 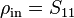 o, para decirlo otra manera, la salida de carga no tiene ningún efecto en la entrada.
o, para decirlo otra manera, la salida de carga no tiene ningún efecto en la entrada.
Una propiedad similar existe en la dirección opuesta, en este caso si 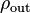 es el coeficiente de reflexión en el puerto de salida y
es el coeficiente de reflexión en el puerto de salida y  es el coeficiente de reflexión de la fuente conectada al puerto de entrada.
es el coeficiente de reflexión de la fuente conectada al puerto de entrada.
Puerto de carga las condiciones para un amplificador para ser incondicionalmente estable
Un amplificador es incondicionalmente estable si una carga o fuente de cualquier coeficiente de reflexión puede conectarse sin causar inestabilidad. Esta condición ocurre si las magnitudes de los coeficientes de reflexión en la fuente, la carga y el amplificador de entrada y salida puertos son al mismo tiempo menos de unidad. Un requisito importante que a menudo se pasa por alto es que el amplificador sea una red linear con no polacos en la mitad derecha del avión.[19] La inestabilidad puede causar distorsión severa de respuesta de frecuencia de ganancia del amplificador o, en el extrema, oscilación. Para ser incondicionalmente estable en la frecuencia de interés, un amplificador debe satisfacer las siguientes 4 ecuaciones simultáneamente:[20]
La condición límite para cuando cada uno de estos valores es igual a la unidad puede ser representada por un círculo dibujado en el Diagrama polar que representa el coeficiente de reflexión (complejo), uno para el puerto de entrada y el otro para el puerto de salida. A menudo éstos se escalarán como cartas de Smith. En cada caso las coordenadas del círculo de centro y el radio asociado se dan por las siguientes ecuaciones:
 valores de
valores de  (círculo de estabilidad de salida)
(círculo de estabilidad de salida)
Radio 
Centro 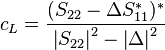
 valores de
valores de  (círculo de estabilidad entrada)
(círculo de estabilidad entrada)
Radio 
Centro 
¿Dónde, en ambos casos
y la estrella superíndice (*) indica una complejo conjugado.
Los círculos son en unidades complejas del coeficiente de reflexión para que puedan extraerse de impedancia o admitancia basado Smith gráficos normalizados para la impedancia del sistema. Esto sirve para mostrar fácilmente las regiones de impedancia normalizada (o ingreso) para la estabilidad incondicional predicha. Otra forma de demostrar la estabilidad incondicional es mediante la estabilidad Rollet factor ( ), definido como
), definido como
La condición de estabilidad incondicional se logra cuando 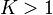 y
y 
Parámetros de dispersión transferencia
Los parámetros de dispersión transferencia o T-parámetros de una red de 2 puertos son expresados por la matriz del parámetro T y están estrechamente relacionados con la matriz de parámetros S correspondiente. La matriz T-parámetro está relacionada con el incidente y refleja las ondas normalizadas en cada uno de los puertos de la siguiente manera:
Sin embargo, se podrían definir diferentemente, como sigue:
El complemento de RF Toolbox para MATLAB[21] y varios libros (por ejemplo "red parámetros de dispersión"[22]) usar esta última definición, así que es necesario tener precaución. Los párrafos "De S a T" y "De T a S" en el presente artículo se basan en la primera definición. Adaptación a la segunda definición es trivial (intercambio de T11 para T22y T12 para T21). La ventaja de T-parámetros en comparación con parámetros de S es que puede utilizarse para determinar fácilmente el efecto de cascada 2 o más redes de 2 puertos simplemente multiplicando las matrices de parámetros T individuales asociadas. Si los parámetros de T de decir tres diferentes 2 puertos redes 1, 2 y 3 son  ,
,  y
y  respectivamente entonces la matriz de T-parámetro de la cascada de todos (tres redes
respectivamente entonces la matriz de T-parámetro de la cascada de todos (tres redes ) en orden serial viene dada por:
) en orden serial viene dada por:
Como con parámetros de S, T-parámetros son complejos y hay una conversión directa entre los dos tipos. Aunque los parámetros de T en cascada es una multiplicación de la matriz simple de las T-parámetros individuales, la conversión para S-parámetros de cada red a los correspondientes parámetros de T y la conversión de los parámetros de T en cascada hacia las cascada S-parámetros equivalentes, que son generalmente necesarios, no es trivial. Sin embargo una vez completada la operación, se tomarán en cuenta las interacciones complejas de onda completa entre todos los puertos en ambas direcciones. Las ecuaciones siguientes proporcionan la conversión entre parámetros S y T para redes de 2 puertos.[23]
De S a T:
De T a S
Donde  indica la determinante de la matriz
indica la determinante de la matriz  .
.
S-parámetros de 1 puerto
El parámetro-S para una red de 1 puerto viene dada por una simple matriz de 1 x 1 de la forma  donde n es el número de puerto asignado. Para cumplir con la definición del parámetro-S de linealidad, normalmente sería una carga pasiva de algún tipo.
donde n es el número de puerto asignado. Para cumplir con la definición del parámetro-S de linealidad, normalmente sería una carga pasiva de algún tipo.
Matrices de S-parámetro de orden superior
S-parámetros para pares de diferentes puertos (de orden superior ), donde
), donde  puede deducir de manera similar a los de 2 puertos redes considerando pares de puertos a su vez, en cada caso, asegurando que todos los restantes puertos (sin usar) se cargan con una impedancia idéntica a la impedancia del sistema. De esta manera la onda incidente energía para cada uno de los puertos no utilizados se convierte en cero rendimiento expresiones similares a los obtenidos para el caso de 2 puertos. S-parámetros relativos a puertos individuales (solamente
puede deducir de manera similar a los de 2 puertos redes considerando pares de puertos a su vez, en cada caso, asegurando que todos los restantes puertos (sin usar) se cargan con una impedancia idéntica a la impedancia del sistema. De esta manera la onda incidente energía para cada uno de los puertos no utilizados se convierte en cero rendimiento expresiones similares a los obtenidos para el caso de 2 puertos. S-parámetros relativos a puertos individuales (solamente ) requiere que todos los restantes puertos para ser cargado con una impedancia idéntica a la impedancia del sistema por lo tanto, hacer todas las ondas de energía incidente cero excepto para el puerto bajo consideración. En general, por tanto, tenemos:
) requiere que todos los restantes puertos para ser cargado con una impedancia idéntica a la impedancia del sistema por lo tanto, hacer todas las ondas de energía incidente cero excepto para el puerto bajo consideración. En general, por tanto, tenemos:
y
Por ejemplo, una red de 3 puertos como un divisor de 2 vías tendrían las siguientes definiciones de parámetro S
Medición de parámetros de S

Analizador de redes vectoriales
El diagrama muestra las partes esenciales de un típico 2-port Analizador de redes vectoriales (VNA). Los dos puertos de la dispositivo bajo prueba (DUT) son denotadas puerto 1 (P1) y puerto 2 (P2). El puerto de prueba conectores proporcionan en el VNA misma son tipos de precisión que normalmente debe ser extendido y conectado a P1 y P2 usando cables de precisión 1 y 2, CP1 y CP2 respectivamente y adaptadores de conector adecuado A1 y A2 respectivamente.
La frecuencia de prueba es generada por una variable de la frecuencia CW fuente y su nivel de potencia se establece mediante una variable Atenuador. La posición del interruptor SW1 fija el sentido de que la señal de prueba atraviesa el DUT. Inicialmente considerar que SW1 está en la posición 1 para que la señal de prueba es incidente en el DUT en P1 que es apropiado para la medición  y
y 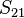 . La señal de prueba es alimentada por SW1 al puerto común del divisor 1, un brazo (el canal de referencia) alimenta un receptor de referencia para P1 (RX referencia1) y el otro (el canal de ensayo) conectando a P1 mediante el acoplador direccional DC1, PC1 y A1. Las tercer puerto de DC1 parejas fuera de la alimentación se refleja en el P1 vía A1 y PC1, entonces para probar el receptor (RX Prueba1) 1. Del mismo modo, señales P2 dejando pasan a través de A2, PC2 y DC2 a RX TEST2. RX REF1, RX Prueba1, RX REF2 y RXTEST2 son conocidos como coherente los receptores ya que comparten el mismo oscilador de referencia, y son capaces de medir la amplitud de la señal de prueba y fase con la frecuencia de prueba. Todo el complejo receptor de salida de las señales son alimentadas a un procesador que realiza el procesamiento matemático y muestra los parámetros elegidos y formato en la pantalla de fase y amplitud. El instantánea valor de fase incluye tanto la temporal y espacial partes, pero el primero es eliminado en virtud de utilizar 2 canales de prueba, uno como una referencia y el otro para la medición. Cuando SW1 se ajusta a la posición 2, las señales de prueba se aplica a P2, la referencia se mide por RX REF2, reflexiones de P2 son juntados apagado por DC2 y medidos por RX TEST2 y señales dejando P1 son juntadas apagado por DC1 y medidas por RX prueba1. Esta posición es apropiada para la medición
. La señal de prueba es alimentada por SW1 al puerto común del divisor 1, un brazo (el canal de referencia) alimenta un receptor de referencia para P1 (RX referencia1) y el otro (el canal de ensayo) conectando a P1 mediante el acoplador direccional DC1, PC1 y A1. Las tercer puerto de DC1 parejas fuera de la alimentación se refleja en el P1 vía A1 y PC1, entonces para probar el receptor (RX Prueba1) 1. Del mismo modo, señales P2 dejando pasan a través de A2, PC2 y DC2 a RX TEST2. RX REF1, RX Prueba1, RX REF2 y RXTEST2 son conocidos como coherente los receptores ya que comparten el mismo oscilador de referencia, y son capaces de medir la amplitud de la señal de prueba y fase con la frecuencia de prueba. Todo el complejo receptor de salida de las señales son alimentadas a un procesador que realiza el procesamiento matemático y muestra los parámetros elegidos y formato en la pantalla de fase y amplitud. El instantánea valor de fase incluye tanto la temporal y espacial partes, pero el primero es eliminado en virtud de utilizar 2 canales de prueba, uno como una referencia y el otro para la medición. Cuando SW1 se ajusta a la posición 2, las señales de prueba se aplica a P2, la referencia se mide por RX REF2, reflexiones de P2 son juntados apagado por DC2 y medidos por RX TEST2 y señales dejando P1 son juntadas apagado por DC1 y medidas por RX prueba1. Esta posición es apropiada para la medición  y
y  .
.
Calibración
Antes de una medición de parámetros VNA S, es el primer paso esencial para llevar a cabo una precisa calibración adecuado a las medidas previstas. Varios tipos de calibración están normalmente disponibles en el VNA. Sólo en los últimos años que VNAs han tenido los suficientemente avanzados está procesando la capacidad, a un costo realista, necesaria para lograr los tipos más avanzados de calibración, incluyendo correcciones para errores sistemáticos.[24] Los tipos más básicos, a menudo llamados calibraciones 'respuesta', pueden realizarse rápidamente pero sólo proporcionará un resultado moderado incertidumbre. Para mayor incertidumbre y rango dinámico de la medida una calibración completa 2 puertos es requerida antes de medición DUT. Efectivamente esto eliminará todas las fuentes de errores sistemáticos inherentes en el sistema de medición de VNA.
Minimización de errores sistemáticos
Errores sistemáticos son aquellos que no varían con el tiempo durante una calibración. Para un conjunto de 2 puertos S-parámetro medidas allí son un total de 12 tipos de errores sistemáticos que son medidos y matemáticamente eliminados como parte del procedimiento de calibración completa 2 puertos. Son, para cada puerto:
1. Directividad y diafonía
2. fuente y carga desajustes
3. respuesta de frecuencia errores causados por la reflexión y transmisión de seguimiento dentro de los receptores de prueba
El procedimiento de calibración requiere inicialmente estableciendo la VNA con todos los cables, adaptadores y conectores necesarios para conectar el DUT pero no en esta etapa conectarlo. Se utiliza un kit de calibración según los tipos de conectores montados en el DUT. Esto normalmente se incluyen adaptadores, cortocircuitos nominales (SCs), abrir circuitos (OCs) y carga estándares de terminación (término) de ambos sexos conector apropiados a los conectores VNA y DUT. Incluso con estándares de alta calidad, al realizar las pruebas en las frecuencias más altas en la gama de microondas diferentes capacitancias callejeros y las inductancias se evidenciarán y causar incertidumbre durante la calibración. Los datos relativos a los perros callejeros del kit de calibración particular utilizado se miden en la fábrica trazable a estándares nacionales y los resultados están programados en la memoria VNA antes de realizar la calibración.
El procedimiento de calibración es normalmente software controlado e instruye al operador para adaptarse a diversos patrones de calibración para los extremos de la DUT los cables de conexión, así como realizar una conexión a través. En cada paso el procesador VNA captura datos en toda la gama de frecuencia de prueba y almacena. Al final del procedimiento de calibración, el procesador utiliza los datos almacenados así obtenidos para aplicar las correcciones de error sistemático a todas las mediciones posteriores hechas. Todas las mediciones posteriores son conocidas como 'corregido medidas'. En este punto el DUT está conectado y una medida corregida de sus S-parámetros.
Formato de salida de datos S-parámetro medidos y corregidos
Los datos de prueba S-parámetro pueden ser proporcionados en muchos formatos alternativos, por ejemplo: la lista, (gráficaCarta de Smith o Diagrama polar).
Formato de lista
En formato de lista los parámetros medidos y corregidos de S se tabulan contra frecuencia. El formato de lista más común se conoce como piedra de toque o SNP, donde N es el número de puertos. Comúnmente los archivos de texto que contiene esta información tendría la extensión de nombre de archivo '.s2p'. Un ejemplo de un Archivo de Touchstone a continuación se muestra el listado para los datos de parámetro S completo 2 puertos obtenidos para un dispositivo:
! Creada Fri 21 de Jul 14:28:50 # 2005 MHZ S DB R 50! SP1.-15.4 SP 50 100,2 10.2 173,5-30.1 9,6 13.4 57,2 51-15.8 103,2 10.7 177,4-33.1 9,6-12.4 63,4 52 15.9 105,5 11.2 179,1-35.7 9,6-14.4 66.9 53-16.4 107,0 10.5 183,1-36.6 9,6-14.7 70.3 54-16.6 109,3 10.6 187,8-38.1 9,6-15.3 71,4
Comenzando con una exclamación de filas contiene sólo Comentarios. El principio de la fila con el símbolo hash indica que en este caso son las frecuencias en megahercios (MHZ), S-parámetros aparecen (S), magnitudes son en magnitud de registro dB (DB) y la impedancia del sistema es de 50 ohmios (R 50). Hay 9 columnas de datos. Columna 1 en este caso es la prueba de frecuencia en megahertz. Columnas 2, 4, 6 y 8 son las magnitudes de  ,
, 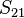 ,
,  y
y  respectivamente en dB. Columnas de 3, 5, 7 y 9 son los ángulos de
respectivamente en dB. Columnas de 3, 5, 7 y 9 son los ángulos de  ,
, 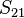 ,
,  y
y  respectivamente en grados.
respectivamente en grados.
Gráfico (carta de Smith)
Cualquier parámetro-S 2 puertos puede visualizarse en un Carta de Smith usando coordenadas polares, pero la más significativa sería  y
y  desde cualquiera de estas puede convertir directamente en una impedancia normalizada equivalente (o ingreso) utilizando la carta de Smith impedancia característica (o ingreso) escala apropiada a la impedancia del sistema.
desde cualquiera de estas puede convertir directamente en una impedancia normalizada equivalente (o ingreso) utilizando la carta de Smith impedancia característica (o ingreso) escala apropiada a la impedancia del sistema.
Gráfico (Diagrama polar)
Cualquier parámetro-S 2 puertos puede visualizarse en un diagrama polar usando coordenadas polares.
En cualquier formato gráfico cada parámetro S a una frecuencia de prueba en particular se muestra como un punto. Si la medición es un barrido a través de varias frecuencias aparecerá un punto para cada uno. Muchos VNAs conectan puntos sucesivos con líneas rectas para la visibilidad fácil.
Medición de parámetros de S de una red de un puerto
La matriz de parámetros S para una red con sólo un puerto tendrá un elemento representado en forma 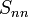 , donde n es el número asignado al puerto. Mayoría VNAs proporcionan una capacidad simple de un puerto de calibración para la medición de un puerto ahorrar tiempo si eso es lo que se requiere.
, donde n es el número asignado al puerto. Mayoría VNAs proporcionan una capacidad simple de un puerto de calibración para la medición de un puerto ahorrar tiempo si eso es lo que se requiere.
S-parámetros de medición de redes con más de 2 puertos
VNAs diseñados para la medida simultánea de los parámetros de S de las redes con más de dos puertos son factibles, pero rápidamente ser prohibitivamente caro y complejo. Generalmente su compra no está justificada ya que las mediciones necesarias pueden obtenerse usando un VNA calibrado estándar de 2 puertos con mediciones más seguidas por la correcta interpretación de los resultados obtenidos. La matriz S-parámetro requerida puede ser montada de mediciones sucesivas de dos puertos en etapas, dos puertos a la vez, en cada ocasión con los puertos no utilizados que finalicen en las cargas de alta calidad iguales a la impedancia del sistema. Un riesgo de este enfoque es que la pérdida de retorno o VSWR de las cargas se debe ser adecuadamente especificado para estar lo más cerca posible a un perfecto 50 Ohms, o sea la impedancia nominal del sistema. Para una red con muchos puertos puede ser una tentación, por razones de costo, para especificar inadecuadamente los VSWRs de las cargas. Algunos análisis será necesario determinar cuál va a ser el peor de los casos Roe aceptable de las cargas.
Suponiendo que las cargas adicionales se especifican adecuadamente, si es necesario, dos o más de los subíndices S-parámetro son modificadas de las relativas a la VNA (1 y 2 en el caso considerado anteriormente) a aquellos relativos a la red bajo prueba (de 1 a N, si N es el número total de puertos DUT). Por ejemplo, si el DUT tiene 5 puertos y un dos VNA está conectado con el puerto de VNA 1 a DUT Puerto 3 y VNA 2 Puerto DUT 5, la medida VNA resultados) ,
,  ,
, 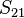 y
y  ) sería equivalente a
) sería equivalente a  ,
,  ,
,  y
y  respectivamente, suponiendo que los puertos DUT 1, 2 y 4 fueron terminados en cargas adecuadas 50 ohmios. Esto proporcionaría 4 de los 25 S-parámetros necesarios.
respectivamente, suponiendo que los puertos DUT 1, 2 y 4 fueron terminados en cargas adecuadas 50 ohmios. Esto proporcionaría 4 de los 25 S-parámetros necesarios.
Véase también
- Parámetros de admisión
- Parámetros de impedancia
- Red de dos puertos
- X-parámetros, un superconjunto de S-parámetros no lineal
- Teorema de Belevitch
Referencias
- ^ Pozar, David M. (2005); Microondas ingeniería, tercera edición (Ed. Intl.); John Wiley & Sons, Inc.; págs. 170-174. ISBN 0-471-44878-8.
- ^ Pozar, David M. (2005) (op. cit.); págs. 170-174.
- ^ Pozar, David M. (2005) (op. cit.); págs. 183-186.
- ^ Morton, A. H. (1985); Avanzada ingeniería eléctrica; Pitman Publishing Ltd.; págs. 33-72. ISBN 0-273-40172-6.
- ^ Belevitch, Vitold "Resumen de la historia de la teoría de circuitos", Actas de la ira, Vol.50, iss.5, págs. 848 – 855, mayo de 1962.
Vandewalle, Joos "In memoriam – Vitold Belevitch", Revista Internacional de teoría de circuitos y aplicaciones, Vol.28, iss.5, págs. 429-430, septiembre/octubre de 2000. - ^ Valkenburg, Mac Elwyn Van Teoría de circuitos: Fundaciones y contribuciones clásicas, p.334, Stroudsburg, Pennsylvania: Dowden, Hutchinson & Ross, 1974 ISBN 0-87933-084-8.
- ^ J. appl. Phys 18, 873 (1947); doi: 10.1063/1.1697561 un método computacional aplicables a redes de microondas R. H. Dicke
- ^ "Salón de la fama parte III de microondas". Microondas 101. PN diseños. 2012. 09 de diciembre de 2012.
- ^ Pozar, David M. (2005) (op. cit.); p. 170.
- ^ Morton, A. H. (1985) (op. cit.); p. 33.
- ^ Kurokawa, K., "Olas de energía y la matriz de dispersión", IEEE trans Micr. Teoría & Tech., marzo de 1965, págs. 194-202
- ^ Pozar, David M. (2005) (op. cit.); p. 173.
- ^ Thomas J. & Chen W.K. (2007). Redes de retroalimentación: aplicaciones de la teoría y el circuito. Singapur: Mundo científico. Capítulo 3, p. 225 ff. ISBN981-02-2770-1.
- ^ Collin, Robert E.; Fundamentos de ingeniería de microondas, segunda edición
- ^ Trevor S. Bird, "Definición y uso indebido de pérdida de retorno", IEEE antenas y propagación Magazine, Vol.51, iss.2, pp.166-167, abril de 2009.
- ^ Backplane canales y correlación entre la frecuencia y el funcionamiento del dominio de tiempo
- ^ Bockelmann, DE y Eisenstadt, WR "combinadas de parámetros de dispersión de modo diferencial y común: teoría y simulación," MTT, parte de IEEE transacciones volumen 43 número 7 1 – 2 de julio de 1995 páginas 1530-1539
- ^ Gonzalez, Guillermo (1997); Análisis de amplificadores de Transistor de microondas y diseño, segunda edición; Prentice Hall NJ; PP 212-216. ISBN 0-13-254335-4.
- ^ J.M. Rollett, "Estabilidad y ganancia de potencia invariantes de dos puertos lineales", IRE trans. circuito teoría vol. CT-9, págs. 29-32, marzo de 1962
- ^ Gonzalez, Guillermo (op. cit.); PP 217-222
- ^ "Documentación de RF Toolbox".
- ^ R. Mavaddat. (1996). Parámetro de dispersión de red. Singapur: Mundo científico. ISBN978-981-02-2305-2.
- ^ S-parámetro diseño; Nota de aplicación un 154; Agilent Technologies; p 14
- ^ Aplicación de corrección de errores a las mediciones de analizador de red; Agilent aplicación nota un 1287-3, Agilent Technologies; P6
Bibliografía
- Guillermo Gonzalez, "microondas amplificadores con transistores, análisis y diseño, 2do. Ed. ", Prentice Hall, New Jersey; ISBN 0-13-581646-7
- David M. Pozar, "Ingeniería de microondas", tercera edición, John Wiley & Sons Inc.; ISBN 0-471-17096-8
- William Eisenstadt, Bob Stengel y Bruce Thompson, "Diseño de circuito diferencial microondas usign parámetros S Mixed-Mode", Artech House; ISBN 1-58053-933-5; ISBN 978-1-58053-933-3
- "S-parámetro de diseño", aplicación nota un 154, Agilent Technologies
- "S-parámetro técnicas para más rápido, más preciso diseño de red", nota de aplicación AN 95-1, Agilent Technologies, PDF se desliza más vídeo QuickTime o Análisis del artículo original de Richard W. Anderson
- A. J. Baden Fuller, "An Introduction to Microwave Theory and técnicas, segunda edición, biblioteca internacional de Pergammon; ISBN 0-08-024227-8
- Ramo, Whinnery y Van Duzer, "Campos y ondas en electrónica de comunicaciones", John Wiley & Sons; ISBN 0-471-70721-X
- C. W. Davidson, "Líneas de transmisión para las comunicaciones con programas CAD", segunda edición, Macmillan educación Ltd.; ISBN 0-333-47398-1



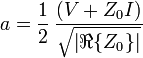


 .
.

 .
.
 y
y
 .
.
 y
y

 .
.
 .
.
 dB.
dB.
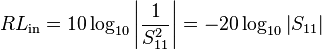 dB.
dB.
 dB.
dB.
 dB.
dB.
 dB.
dB.
 .
.
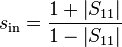



 .
.

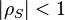


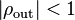
 (círculo de estabilidad de salida)
(círculo de estabilidad de salida) valores de
valores de  (círculo de estabilidad entrada)
(círculo de estabilidad entrada)