Cuantización (procesamiento de señal)

Cuantización, en matemáticas y procesamiento de señal digital, es el proceso de asignación de un amplio conjunto de valores de entrada a un (contable) más pequeño conjunto – tales como redondeo valores de alguna unidad de precisión. Un dispositivo o función algorítmica que realiza la cuantización es llamado un cuantificador. El error de redondeo introducido por cuantización se denomina error de cuantización.
En conversión de analógico a digital, se llama la diferencia entre el real valor analógico y digital quantized error de cuantización o distorsión de cuantificación. Este error es debido a redondeo o truncamiento. La señal de error a veces es modelada como una señal aleatoria adicional llamada ruido de cuantización debido su estocástico comportamiento. Cuantización participa en cierto grado en casi todo el procesamiento de señal digital, como el proceso de representar una señal en forma digital normalmente implica el redondeo. Cuantización forma también la base esencialmente todos tipo de compresión algoritmos.
Contenido
- 1 Las propiedades básicas y tipos de cuantización
- 2 Cuantización escalar
- 3 Ejemplo de redondeo
- 4 Canalización vertical medio y medio pisadas uniformes quantizers
- 5 Distorsión granular y distorsión de sobrecarga
- 6 El modelo de ruido aditivo para el error de cuantización
- 7 Modelos de error de cuantización
- 8 Modelo de ruido de cuantización
- 9 Diseño de tarifa – distorsión cuantificador
- 10 Descuidar la restricción de la entropía: cuantización Lloyd – Max
- 11 Cuantización uniforme y la aproximación de 6 dB/bit
- 12 Otros campos
- 13 Véase también
- 14 Notas
- 15 Referencias
- 16 Enlaces externos
Las propiedades básicas y tipos de cuantización
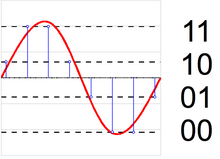
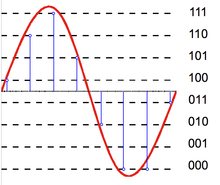
Cuantización es una asignación de muchos-a-pocos, es un inherentemente no-lineal y el proceso irreversible (es decir, porque el mismo valor de salida es compartido por varios valores de entrada, es imposible en general para recuperar el valor exacto de entrada cuando se administra solamente el valor de salida).
El conjunto de valores posibles de entrada puede ser infinitamente grande y puede ser continuo y por lo tanto incontables (por ejemplo, el conjunto de todos números realeso todos los números reales dentro de algunas gama limitada). El conjunto de valores posibles de salida puede ser finito o contable infinito. Los conjuntos de entrada y salidos en cuantización pueden definirse de una manera bastante general. Por ejemplo, Vector quantization es la aplicación de cuantización para entrada de datos multidimensional (vector-valorado).[2]
Existen dos clases sustancialmente diferentes de las aplicaciones donde se utiliza la cuantización:
- El primer tipo, que puede ser llamado simplemente redondeo Cuantización, es la empleada para que muchas aplicaciones, para permitir el uso de una simple representación aproximada para una cantidad que se va a ser medido y utilizados en otros cálculos. Esta categoría incluye las aproximaciones redondeo simples usadas en aritmética diaria. Esta categoría también incluye conversión de analógico a digital de una señal para un sistema de procesamiento de señal digital (por ejemplo, usando una tarjeta de sonido de un ordenador personal para captar una señal de audio) y los cálculos realizaron dentro de los procesos de filtrado digitales más. Aquí el objetivo es principalmente para conservar tanta fidelidad de señal posible mientras eliminando precisión innecesario y mantener el rango dinámico de la señal dentro de límites prácticos (para evitar la señal recorte o desbordamiento aritmético). En tales aplicaciones, pérdida substancial de la fidelidad de la señal a menudo es inaceptable, y el diseño a menudo se centra en gestionar el error de aproximación para garantizar que se introduce distorsión muy poco.
- El segundo tipo, que puede llamarse tarifa – distorsión optimizado Cuantización, se encuentra en codificación de fuente algoritmos de compresión de datos "con pérdida", donde el propósito es gestionar distorsión dentro de los límites de la velocidad de bits apoyada por un medio de almacenamiento o canal de comunicación. En esta segunda opción, la cantidad de distorsión introducida puede gestionarse cuidadosamente por técnicas sofisticadas y presentando una significativa cantidad de distorsión puede ser inevitable. Un cuantificador diseñado para este propósito puede ser bastante diferente y más elaborada en el diseño de una operación de redondeo ordinaria. Es en este ámbito tan importante teoría de tarifa – distorsión el análisis es probable ser aplicado. Sin embargo, los mismos conceptos se aplican realmente en ambos casos de uso.
El análisis de cuantización implica estudiar la cantidad de datos (normalmente medidos en dígitos o bits o bit tasa) que se utiliza para representar la salida del cuantificador y estudiar la pérdida de precisión que se introduce por el proceso de cuantización (que se conoce como el distorsión). El general campo de estudio de este tipo de tasa y distorsión es conocido como teoría de tarifa – distorsión.
Cuantización escalar
El tipo más común de cuantización es conocido como Cuantización escalar. Cuantización escalar, típicamente denotado como  , es el proceso mediante una función de cuantización
, es el proceso mediante una función de cuantización  () para asignar un valor escalar de entrada (unidimensional)
() para asignar un valor escalar de entrada (unidimensional)  a un valor de salida escalar
a un valor de salida escalar  . Cuantización escalar puede ser tan simple e intuitiva como redondeo alta precisión los números al entero más próximo o al múltiplo más cercano de alguna otra unidad de precisión (por ejemplo, redondeando una gran cantidad monetaria a los miles de dólares más cercanos). Cuantización escalar continua valores de datos de entrada que se realizaron por una vía electrónica sensor se denomina conversión de analógico a digital. A menudo también implica la conversión de analógico a digital muestreo la señal periódicamente en el tiempo (por ejemplo, en 44.1 kHz para CD-las señales de audio de calidad).
. Cuantización escalar puede ser tan simple e intuitiva como redondeo alta precisión los números al entero más próximo o al múltiplo más cercano de alguna otra unidad de precisión (por ejemplo, redondeando una gran cantidad monetaria a los miles de dólares más cercanos). Cuantización escalar continua valores de datos de entrada que se realizaron por una vía electrónica sensor se denomina conversión de analógico a digital. A menudo también implica la conversión de analógico a digital muestreo la señal periódicamente en el tiempo (por ejemplo, en 44.1 kHz para CD-las señales de audio de calidad).
Ejemplo de redondeo
Por ejemplo, redondeo un número real  al valor entero más cercano formas un tipo básico de cuantificador – un uniforme uno. Un típico (banda de rodadura media) cuantificador uniforme con una cuantificación tamaño de paso igual a algún valor
al valor entero más cercano formas un tipo básico de cuantificador – un uniforme uno. Un típico (banda de rodadura media) cuantificador uniforme con una cuantificación tamaño de paso igual a algún valor  puede ser expresado como
puede ser expresado como
-
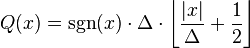 ,
,
donde la función  () es el función signo (también conocido como el Signum función). Por simple redondeo al entero más cercano, el tamaño de paso
() es el función signo (también conocido como el Signum función). Por simple redondeo al entero más cercano, el tamaño de paso  es igual a 1. Con
es igual a 1. Con  o con
o con  igual a cualquier otro valor entero, este cuantificador tiene valor real entradas y salidas de valores enteros, aunque esta propiedad no es una necesidad – un cuantificador tenga también un entero dominio de entrada y también pueden haber no enteros salida de valores. La característica esencial de un cuantificador es que tiene un sistema contable de los valores de salida posible que tiene menos miembros que el conjunto de posibles valores de entrada. Los miembros del conjunto de los valores de salida pueden tener valores enteros, racionales, o real (o incluso otros posibles valores así como, en general – como los valores del vector o números complejos).
igual a cualquier otro valor entero, este cuantificador tiene valor real entradas y salidas de valores enteros, aunque esta propiedad no es una necesidad – un cuantificador tenga también un entero dominio de entrada y también pueden haber no enteros salida de valores. La característica esencial de un cuantificador es que tiene un sistema contable de los valores de salida posible que tiene menos miembros que el conjunto de posibles valores de entrada. Los miembros del conjunto de los valores de salida pueden tener valores enteros, racionales, o real (o incluso otros posibles valores así como, en general – como los valores del vector o números complejos).
Cuando el tamaño de paso de cuantización es pequeño (en relación con la variación de la señal de medición), es relativamente sencillo Mostrar[3][4][5][6][7][8] que el error al cuadrado es decir producido por tal una operación de redondeo será aproximadamente  . Error cuadrado medio también se llama la cuantización potencia de ruido. Agregando un poco a las mitades del cuantificador el valor de Δ, que reduce la potencia de ruido por el factor de ¼. En términos de decibelios, es el cambio de potencia de ruido
. Error cuadrado medio también se llama la cuantización potencia de ruido. Agregando un poco a las mitades del cuantificador el valor de Δ, que reduce la potencia de ruido por el factor de ¼. En términos de decibelios, es el cambio de potencia de ruido
Porque el conjunto de valores posibles de un cuantificador es contable, cualquier cuantificador se puede descomponer en dos etapas distintas, que pueden ser referidas como el clasificación etapa (o Cuantización hacia adelante etapa) y la reconstrucción etapa (o quantization inverso etapa), donde la fase de clasificación asigna el valor de entrada a un entero Índice de cuantización  y la etapa de reconstrucción asigna el índice
y la etapa de reconstrucción asigna el índice  para el valor de reconstrucción
para el valor de reconstrucción 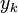 es la aproximación de salida del valor de entrada. Para el cuantificador uniforme de ejemplo descrito anteriormente, la etapa de cuantificación directa puede ser expresada como
es la aproximación de salida del valor de entrada. Para el cuantificador uniforme de ejemplo descrito anteriormente, la etapa de cuantificación directa puede ser expresada como
-
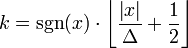 ,
,
y la etapa de reconstrucción para la cuantificación de este ejemplo es simplemente  .
.
Esta descomposición es útil para el diseño y análisis del comportamiento de cuantización, e ilustra cómo pueden ser comunicados los datos cuantificados por un canal de comunicación – un codificador fuente puede realizar la etapa de cuantificación directa y enviar la información de índice a través de un canal de comunicación (posiblemente aplicar codificación de la entropía técnicas a los índices de cuantización) y un decodificador puede realizar la etapa de reconstrucción para producir la aproximación de la salida de los datos de entrada originales. En diseños más elaborados de cuantización, ambas etapas la cuantificación directa e inversa pueden ser substancialmente más complejas. En general, la etapa de cuantificación directa puede utilizar cualquier función que asigna los datos de entrada al espacio entero de los datos de índice de cuantización, y la etapa del quantization inverso puede expresiones (o literalmente) una operación de búsqueda de mesa para asignar cada índice de cuantización a un valor de reconstrucción correspondiente. Esta descomposición de dos etapas se aplica igualmente bien a Vector así como quantizers escalares.
Canalización vertical medio y medio pisadas uniformes quantizers
Más uniformes quantizers para entrada de datos firmado pueden clasificarse como de uno de dos tipos: Mid-Riser y banda de rodadura media. La terminología se basa en lo que sucede en la región alrededor del valor 0 y utiliza la analogía de la visualización de la función de entrada y salida del cuantificador como un escalera. Pisada mediados quantizers tienen un nivel de reconstrucción de valor cero (correspondiente a un banda de rodadura de una escalera), mientras que medio verticales quantizers tienen un umbral de clasificación valor cero (correspondiente a un canalización vertical de una escalera).[9]
Las fórmulas de cuantización uniforme pisada medio están indicadas.
La fórmula de entrada y salida para un cuantificador uniforme vertical media viene dada por:
-
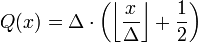 ,
,
donde la regla de clasificación está dada por
y la regla de reconstrucción es
-
 .
.
Tenga en cuenta que medio verticales uniformes quantizers no tienen un valor de salida cero – su magnitud mínima salida es la mitad del tamaño de paso. Cuando los datos de entrada pueden ser modelados como una variable aleatoria con un función de densidad de probabilidad (pdf) que es suave y simétrica alrededor de cero, canalización vertical media quantizers también siempre producen una salida entropía de al menos 1 bits por muestra.
En contraste, pisadas mediados quantizers tienen un nivel de salida de cero y pueden alcanzar tasas de bits arbitrariamente por muestra para entrada distribuciones simétricas y forma cónica apagado en magnitudes superiores. Para algunas aplicaciones, puede ser una necesidad tener una representación de señal de salida de cero o apoyando la entropía salida baja. En tales casos, usando un cuantificador uniforme mediados pisada puede ser apropiado durante el uso de un mid-riser uno no sería.
En general, un cuantificador media ascendente o pisada medio no puede ser en realidad un uniforme cuantificador – es decir, el tamaño de los intervalos del cuantificador clasificación puede no ser el mismo, o el espaciado entre los valores de su posible salida puede no ser el mismo. La característica distintiva de un cuantificador medio vertical es que tiene un valor de umbral de clasificación que es exactamente cero, y la característica distintiva de un cuantificador de mediados de la pisada es tiene un valor de reconstrucción que es exactamente cero.[9]
Es otro nombre para un cuantificador de mediados de la pisada cuantificador de zonas muertas, y la región de clasificación alrededor del cero valor de salida de tal un cuantificador es referida como el zona muerta. La zona muerta a veces puede servir el mismo propósito como un puerta de ruido o silenciador función.
Distorsión granular y distorsión de sobrecarga
El diseño de un cuantificador implica a menudo apoyando sólo una gama limitada de los valores de salida posible y la realización de recorte para limitar la salida a esta gama cuando la entrada supera el rango soportado. El error introducido por este recorte se denomina sobrecarga distorsión. Dentro de los límites extremos de la gama soportado, la cantidad de espacio entre los valores de salida seleccionable de un cuantificador se conoce como su granularidad, y el error introducido por este espacio se conoce como granular distorsión. Es común para el diseño de un cuantificador que implican determinar el equilibrio adecuado entre la distorsión granular y distorsión de la sobrecarga. Para un número determinado de apoyo de los valores de salida posible, reducir la distorsión granular promedio puede implicar incrementar la sobrecarga media distorsión y viceversa. Una técnica para controlar la amplitud de la señal (o, equivalente, el tamaño de paso de cuantización  ) lograr el equilibrio adecuado es el uso de control automático de ganancia (AGC). Sin embargo, en algunos diseños de cuantificador, los conceptos de error granular y error de sobrecarga no se apliquen (por ejemplo, para un cuantificador con una gama limitada de datos de entrada o con un conjunto infinito contable de los valores de salida seleccionable).
) lograr el equilibrio adecuado es el uso de control automático de ganancia (AGC). Sin embargo, en algunos diseños de cuantificador, los conceptos de error granular y error de sobrecarga no se apliquen (por ejemplo, para un cuantificador con una gama limitada de datos de entrada o con un conjunto infinito contable de los valores de salida seleccionable).
El modelo de ruido aditivo para el error de cuantización
Una suposición común para el análisis de error de cuantización es que afecta a un sistema de procesamiento de la señal de una manera similar a la de aditivo ruido blanco – tener correlación insignificante con la señal y una aproximadamente plana densidad espectral de potencia.[4][8][10][11] El modelo de ruido aditivo se utiliza comúnmente para el análisis de los efectos de errores de cuantificación en sistemas de filtración digitales, y puede ser muy útil en ese análisis. Se ha demostrado para ser un modelo válido en casos de cuantización de alta resolución (pequeño  en relación a la intensidad de la señal) con funciones de densidad de probabilidad liso.[4][12] Sin embargo, ruido aditivo comportamiento no siempre es una suposición válida, y debe tenerse cuidado para evitar asumir que este modelo se aplica siempre. En la actualidad, el error del quantization (para quantizers definido según lo descrito aquí) determinista está relacionado con la señal en lugar de ser independiente de ella.[8]Por lo tanto, señales periódicas pueden crear ruido de cuantización periódica. Y en algunos casos puede incluso causar ciclos límite que aparecen en los sistemas de procesamiento de señal digital.[11]
en relación a la intensidad de la señal) con funciones de densidad de probabilidad liso.[4][12] Sin embargo, ruido aditivo comportamiento no siempre es una suposición válida, y debe tenerse cuidado para evitar asumir que este modelo se aplica siempre. En la actualidad, el error del quantization (para quantizers definido según lo descrito aquí) determinista está relacionado con la señal en lugar de ser independiente de ella.[8]Por lo tanto, señales periódicas pueden crear ruido de cuantización periódica. Y en algunos casos puede incluso causar ciclos límite que aparecen en los sistemas de procesamiento de señal digital.[11]
Una forma de asegurar la independencia efectiva del error de cuantización de la señal de la fuente es realizar interpolado Cuantización (a veces con forma de ruido), que consiste en agregar al azar (o pseudo-random) ruido a la señal antes de cuantización.[8][11] Esto puede ser beneficioso para propósitos tales como mejora de la calidad subjetiva de los resultados, sin embargo puede aumentar la cantidad total de error introducido por el proceso de cuantización.
Modelos de error de cuantización
En el caso típico, la señal original es mucho mayor que uno bit menos significativo (LSB). Cuando éste es el caso, el error de cuantización no se correlaciona significativamente con la señal y tiene una aproximadamente distribución uniforme. En el caso de redondeo, el error de cuantización tiene una media de cero y el RMS valor es la desviación estándar de esta distribución, dada por  . En el caso de truncamiento del error tiene una media de cero de
. En el caso de truncamiento del error tiene una media de cero de  y el valor RMS es
y el valor RMS es 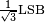 . En cualquier caso, la desviación estándar, como porcentaje de la gama de señal completa, cambia por un factor de 2 para cada cambio de 1-bit en el número de bits de cuantificación. Por lo tanto el cociente signal-to-cuantificación-noise energía potencial cambia por 4, o
. En cualquier caso, la desviación estándar, como porcentaje de la gama de señal completa, cambia por un factor de 2 para cada cambio de 1-bit en el número de bits de cuantificación. Por lo tanto el cociente signal-to-cuantificación-noise energía potencial cambia por 4, o decibelios por poco.
decibelios por poco.
Las amplitudes inferiores el error de cuantificación se convierte en dependiente de la señal de entrada, lo que resulta en distorsión. Esta distorsión se crea después el filtro anti-aliasing, y si estas distorsiones están por encima de 1/2 la frecuencia de muestreo alias apoyará en la banda de interés. Con el fin de independizar el error de cuantización de la señal de entrada, ruido con una amplitud de 2 bits menos significativos se añade a la señal. Esto reduce ligeramente la señal / ruido, pero idealmente, elimina totalmente la distorsión. Es conocido como "dither".
Modelo de ruido de cuantización
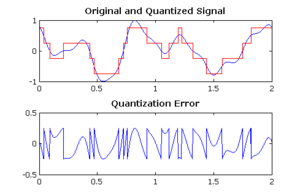
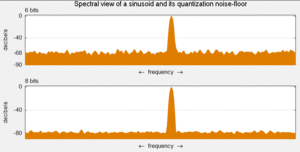
Ruido de cuantización es un modelo del error de cuantización introducida por Cuantización En conversión de analógico a digital (ADC) en sistemas de telecomunicación y procesamiento de señales. Es un error de redondeo entre la tensión de entrada analógica de la ADC y el valor de salida digitalizado. El ruido es no lineal y dependiente de la señal. Se puede modelar en varias formas diferentes.
En un convertidor de analógico a digital ideal, donde el error de cuantificación se distribuye uniformemente entre −1/2 LSB y + 1/2 LSB y la señal tiene una distribución uniforme cubren todos los niveles de cuantificación, la Relación señal a ruido cuantización (SQNR) puede calcularse a partir
Donde Q es el número de bits de cuantificación.
Las señales de prueba más común que cumplen con esto son amplitud completa ondas del triángulo y ondas de diente de Sierra.
Por ejemplo, un 16-bit ADC tiene una relación señal / ruído máxima 6.02 × 16 = 96,3 dB.
Cuando la señal de entrada es una amplitud completa onda de seno la distribución de la señal ya no es uniforme, y la ecuación correspondiente está en su lugar
Aquí está otra vez el ruido de cuantización asume para ser distribuida uniformemente. Cuando la señal de entrada tiene una gran amplitud y un espectro de frecuencias amplia este es el caso.[13] En este caso un 16-bit ADC tiene una relación señal / ruído máxima 98,09 dB. La diferencia en el signal-to-noise 1.761 sólo ocurre debido a la señal es una onda sinusoidal a escala real en lugar de un triángulo/diente de sierra.
Potencia de ruido de cuantización se puede derivar de
donde  es el voltaje del nivel.
es el voltaje del nivel.
(Valores típicos de la vida real son peores que este mínimo teórico, debido a la adición de "dither" para reducir los efectos desagradables de cuantización y a las imperfecciones de la circuitería de ADC. Por otro lado, a menudo usan especificaciones -Ponderado medidas para ocultar los efectos inaudibles de forma de ruidolo que mejora la medición.)
Para señales complejas en alta resolución ADC es un modelo exacto. Baja resolución ADC, señales de bajo nivel en alta resolución ADC y simples formas de onda que del ruido de cuantización no está distribuido uniformemente, haciendo este modelo inexacta.[14] En estos casos la distribución del ruido de cuantización es afectada fuertemente por la amplitud exacta de la señal.
Los cálculos anteriores, sin embargo, suponer un canal de entrada completamente lleno. Si esto no es el caso - si la señal de entrada es pequeña - la distorsión de cuantificación relativa puede ser muy grande. Para eludir esta cuestión, analógica compresores y expansores puede ser utilizado, pero estos introducen grandes cantidades de distorsión, especialmente si el compresor no coincide con el expansor. La aplicación de estos compresores y expansores es también conocido como companding.
Diseño de tarifa – distorsión cuantificador
Un cuantificador escalar, que realiza una operación de cuantización, normalmente se puede descomponer en dos etapas:
- Clasificación: Un proceso que clasifica la gama de la señal de entrada en
 No se superponen intervalos
No se superponen intervalos 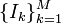 , definiendo
, definiendo 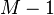 límite (decisión) valores
límite (decisión) valores 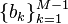 , tal que
, tal que 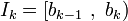 para
para 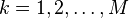 , con los límites extremos definidos por
, con los límites extremos definidos por  y
y  . Todas las entradas
. Todas las entradas  que caen en un rango determinado intervalo
que caen en un rango determinado intervalo 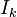 se asocian con el mismo índice de cuantización
se asocian con el mismo índice de cuantización  .
. - Reconstrucción: Cada intervalo
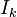 está representado por un valor de reconstrucción
está representado por un valor de reconstrucción 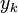 que implementa la asignación
que implementa la asignación 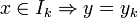 .
.
Estas dos etapas abarcan la operación matemática de  .
.
Codificación de la entropía técnicas pueden ser aplicadas para comunicar a los índices de cuantización de un codificador fuente que realiza la fase de clasificación a un decodificador que realiza la etapa de reconstrucción. Una manera de hacer esto es asociar cada índice de cuantización  con una operación binaria
con una operación binaria 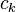 . Una consideración importante es el número de bits usados para cada operación, denotada aquí por
. Una consideración importante es el número de bits usados para cada operación, denotada aquí por 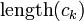 .
.
Como resultado, el diseño de un  -nivel de cuantificador y un conjunto asociado de codewords para comunicar sus valores de índice requiere encontrar los valores de
-nivel de cuantificador y un conjunto asociado de codewords para comunicar sus valores de índice requiere encontrar los valores de 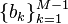 ,
, 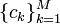 y
y  que satisfacer óptimamente un conjunto seleccionado de restricciones de diseño tales como la tasa de bits
que satisfacer óptimamente un conjunto seleccionado de restricciones de diseño tales como la tasa de bits  y distorsión
y distorsión  .
.
Suponiendo que una fuente de información  produce variables aleatorias
produce variables aleatorias  con un asociado función de densidad de probabilidad
con un asociado función de densidad de probabilidad  , la probabilidad
, la probabilidad 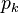 que la variable aleatoria cae dentro de un intervalo de cuantización particular
que la variable aleatoria cae dentro de un intervalo de cuantización particular 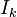 está dada por
está dada por
-
![p_k = P[x \in I_k] = \int_{b_{k-1}}^{b_k} f(x)dx](//upload.wikimedia.org/math/9/1/8/91861058256271d87464b9931c3b9a58.png) .
.
La tasa de bits resultante  , en unidades de bits promedio por valor quantized, para este cuantificador puede obtenerse de la siguiente manera:
, en unidades de bits promedio por valor quantized, para este cuantificador puede obtenerse de la siguiente manera:
-
 .
.
Si se asume que la distorsión se mide por error al cuadrado es decir, la distorsión D, viene dada por:
-
![D = E[(x-Q(x))^2] = \int_{-\infty}^{\infty} (x-Q(x))^2f(x)dx = \sum_{k=1}^{M} \int_{b_{k-1}}^{b_k} (x-y_k)^2 f(x)dx](//upload.wikimedia.org/math/4/9/e/49ee960cd614cd3180061b198772dd46.png) .
.
Tenga en cuenta que también pueden considerarse otras medidas de distorsión, aunque medio cuadrado error es popular.
Una observación clave es que la tasa de  depende de los límites de decisión
depende de los límites de decisión 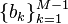 y la longitud de la contraseña
y la longitud de la contraseña  , mientras que la distorsión
, mientras que la distorsión  depende de los límites de decisión
depende de los límites de decisión 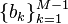 y los niveles de reconstrucción
y los niveles de reconstrucción  .
.
Después de definir estas métricas de dos desempeño para el cuantificador, una formulación de tarifa – distorsión típica para un problema de diseño cuantificador puede expresarse en una de dos maneras:
- Dada una restricción máxima distorsión
 , reducir la tasa de bits
, reducir la tasa de bits 
- Dada una restricción de tasa de bits máxima
 , minimizar la distorsión
, minimizar la distorsión 
A menudo la solución a estos problemas puede ser equivalente (o aproximadamente) expresada y resuelto mediante la conversión de la formulación del problema sin restricciones 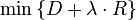 donde el Multiplicadores de Lagrange
donde el Multiplicadores de Lagrange  es una constante no negativo que establece el equilibrio adecuado entre la tasa y distorsión. Para resolver el problema sin restricciones es equivalente a encontrar un punto en el casco convexo de la familia de soluciones a un equivalente había restringida formulación del problema. Sin embargo, encontrar una solución – especialmente un forma cerrada solución – a cualquiera de estas formulaciones tres problema puede ser difícil. Soluciones que no requieren técnicas de optimización iterativa multidimensional se han publicado sólo tres funciones de distribución de probabilidad: el uniforme,[15] exponencial,[16] y Laplaciano[16] distribuciones. Métodos iterativos optimización pueden utilizarse para encontrar soluciones en otros casos.[8][17][18]
es una constante no negativo que establece el equilibrio adecuado entre la tasa y distorsión. Para resolver el problema sin restricciones es equivalente a encontrar un punto en el casco convexo de la familia de soluciones a un equivalente había restringida formulación del problema. Sin embargo, encontrar una solución – especialmente un forma cerrada solución – a cualquiera de estas formulaciones tres problema puede ser difícil. Soluciones que no requieren técnicas de optimización iterativa multidimensional se han publicado sólo tres funciones de distribución de probabilidad: el uniforme,[15] exponencial,[16] y Laplaciano[16] distribuciones. Métodos iterativos optimización pueden utilizarse para encontrar soluciones en otros casos.[8][17][18]
Tenga en cuenta que los valores de reconstrucción  afectan sólo la distorsión – no afectan la tasa de bits – y que cada individuo
afectan sólo la distorsión – no afectan la tasa de bits – y que cada individuo 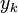 hace una contribución independiente
hace una contribución independiente  a la distorsión total como se muestra abajo:
a la distorsión total como se muestra abajo:
donde
Esta observación puede ser utilizada para facilitar el análisis – dado el conjunto de 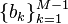 valores, el valor de cada
valores, el valor de cada 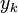 por separado se puede optimizar para minimizar su contribución a la distorsión
por separado se puede optimizar para minimizar su contribución a la distorsión  .
.
Para el criterio de distorsión cuadrado medio del error, puede ser fácilmente demostrado que el conjunto óptimo de reconstrucción valores  está dada por el valor de reconstrucción
está dada por el valor de reconstrucción 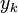 dentro de cada intervalo
dentro de cada intervalo 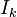 para el valor esperado condicional (también conocido como el centroide) en el intervalo, como determinado por:
para el valor esperado condicional (también conocido como el centroide) en el intervalo, como determinado por:
-
 .
.
El uso de técnicas de codificación de la entropía suficientemente bien diseñado puede resultar en el uso de una tasa de bits que se encuentra cerca de la información veraz de los índices de contenido  , tal que efectivamente
, tal que efectivamente
y por lo tanto
-
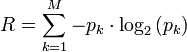 .
.
El uso de esta aproximación puede permitir que el problema de diseño codificación entropía separar el diseño del cuantificador de sí mismo. Entropía moderna técnicas de codificación como codificación aritmética puede alcanzar velocidades de bits que están muy cerca de la verdadera entropía de una fuente, dado un conjunto de probabilidades conocidas (o adaptativa estimados)  .
.
En algunos diseños, en lugar de optimización para un determinado número de regiones de clasificación  , el problema de diseño de cuantificador puede incluir la optimización del valor de
, el problema de diseño de cuantificador puede incluir la optimización del valor de  tan bien. Para algunos modelos probabilísticos fuente, puede ser el mejor rendimiento alcanzado cuando
tan bien. Para algunos modelos probabilísticos fuente, puede ser el mejor rendimiento alcanzado cuando  tiende a infinito.
tiende a infinito.
Descuidar la restricción de la entropía: cuantización Lloyd – Max
En la formulación anterior, si el bitrate restricción se descuida estableciendo  igual a 0, o equivalente si se asume que un código de longitud fija (FLC) se utilizará para representar los datos cuantificados en vez de un Código de longitud variable (o algún otro codificación de la entropía tecnología tales como codificación aritmética es mejor que un FLC en el sentido de ritmo – distorsión), el problema de optimización reduce a la minimización de la distorsión
igual a 0, o equivalente si se asume que un código de longitud fija (FLC) se utilizará para representar los datos cuantificados en vez de un Código de longitud variable (o algún otro codificación de la entropía tecnología tales como codificación aritmética es mejor que un FLC en el sentido de ritmo – distorsión), el problema de optimización reduce a la minimización de la distorsión  sola.
sola.
Los índices producción por un  -nivel cuantificador puede ser codificado utilizando un código de longitud fija
-nivel cuantificador puede ser codificado utilizando un código de longitud fija  bits/símbolo. Por ejemplo cuando
bits/símbolo. Por ejemplo cuando  256 niveles, tasa de bits del FLC
256 niveles, tasa de bits del FLC  es 8 bits/símbolo. Por esta razón, tal un cuantificador a veces ha sido llamado un cuantificador de 8 bits. Sin embargo, usando un FLC elimina la mejora de la compresión que puede ser obtenida por el uso de la codificación de la entropía mejor.
es 8 bits/símbolo. Por esta razón, tal un cuantificador a veces ha sido llamado un cuantificador de 8 bits. Sin embargo, usando un FLC elimina la mejora de la compresión que puede ser obtenida por el uso de la codificación de la entropía mejor.
Suponiendo un FLC con  los niveles, el problema de minimización de tarifa – distorsión pueden reducirse a la minimización de la distorsión sola. El problema reducido puede ser indicado de la siguiente manera: dada una fuente
los niveles, el problema de minimización de tarifa – distorsión pueden reducirse a la minimización de la distorsión sola. El problema reducido puede ser indicado de la siguiente manera: dada una fuente  con PDF
con PDF  y la restricción de que el cuantificador debe utilizar solamente
y la restricción de que el cuantificador debe utilizar solamente  regiones de clasificación, encontrar los límites de decisión
regiones de clasificación, encontrar los límites de decisión 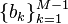 y los niveles de reconstrucción
y los niveles de reconstrucción  para minimizar la distorsión resultante
para minimizar la distorsión resultante
-
![D=E[(x-Q(x))^2] = \int_{-\infty}^{\infty} (x-Q(x))^2f(x)dx = \sum_{k=1}^{M} \int_{b_{k-1}}^{b_k} (x-y_k)^2 f(x)dx =\sum_{k=1}^{M} d_k](//upload.wikimedia.org/math/6/a/8/6a8715dfbc9eec977dcfd8981dea45f6.png) .
.
Encontrar una solución óptima a los resultados anteriores del problema en un cuantificador a veces llamado una solución MMSQE (error de cuantización cuadrada media mínima), y el resultante pdf optimizado (no uniforme) cuantificador se conoce como un Lloyd – Max cuantificador, el nombre de dos personas que desarrollaron independientemente métodos iterativos[8][19][20] para resolver los dos conjuntos de ecuaciones simultáneas resultantes  y
y  , de la siguiente manera:
, de la siguiente manera:
-
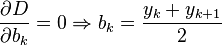 ,
,
que cada umbral sitúa en el punto medio entre cada par de valores de reconstrucción, y
que coloca a cada valor de reconstrucción en el centroide (valor esperado condicional) de su intervalo de clasificación asociada.
Método de Lloyd algoritmo, descrito originalmente en 1957, se puede generalizar en forma del straighforward de aplicación para Vector datos. Esta generalización resulta en la Linde – Buzo – gris (LBG) o k-means métodos de optimización del clasificador. Por otra parte, la técnica se puede generalizar más de una manera sencilla para incluir una restricción de entropía para datos vectoriales.[21]
Cuantización uniforme y la aproximación de 6 dB/bit
El cuantificador Lloyd – Max es en realidad un cuantificador uniforme cuando la entrada PDF se distribuye uniformemente en el rango de  . Sin embargo, por una fuente que no tiene una distribución uniforme, el cuantificador distorsión mínima no puede ser un cuantificador uniforme.
. Sin embargo, por una fuente que no tiene una distribución uniforme, el cuantificador distorsión mínima no puede ser un cuantificador uniforme.
El análisis de un cuantificador uniforme aplicada a una fuente uniformemente distribuida pueden resumirse en lo siguiente:
Una fuente simétrica X puede modelarse con  , para
, para ![x \in [-X_{max} , X_{max}]](http://upload.wikimedia.org/math/0/5/d/05de428a42ebf3117a5aa9dacdce9f70.png) y 0 en otro lugar. El tamaño de paso
y 0 en otro lugar. El tamaño de paso  y el señal / ruido de cuantización (SQNR) es el cuantificador
y el señal / ruido de cuantización (SQNR) es el cuantificador
-
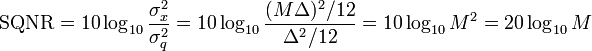 .
.
Para usar un código de longitud fija  pedacitos,
pedacitos,  , dando por resultado
, dando por resultado  ,
,
o aproximadamente 6 dB por poco. Por ejemplo, para  = 8 bits
= 8 bits  = 256 niveles y SQNR = 8 * 6 = 48 dB; y para
= 256 niveles y SQNR = 8 * 6 = 48 dB; y para  = 16 pedacitos,
= 16 pedacitos,  = 65536 y SQNR = 16 * 6 = 96 dB. La propiedad de 6 dB mejora en SQNR para cada extra poco utilizado en la cuantización es una figura muy conocida de mérito. Sin embargo, debe utilizarse con cuidado: esta derivación es sólo para un cuantificador uniforme aplicada a una fuente uniforme.
= 65536 y SQNR = 16 * 6 = 96 dB. La propiedad de 6 dB mejora en SQNR para cada extra poco utilizado en la cuantización es una figura muy conocida de mérito. Sin embargo, debe utilizarse con cuidado: esta derivación es sólo para un cuantificador uniforme aplicada a una fuente uniforme.
Para otros fuente pdfs y otros diseños de cuantificador, el SQNR puede ser algo diferente de la predicha por 6 dB/bit, dependiendo del tipo de pdf, el tipo de fuente, el tipo de cuantificador y el rango de tasa de bits de operación.
Sin embargo, es común suponer que por muchas fuentes, la pendiente de una función SQNR cuantificador se puede aproximar como 6 dB/bit cuando opera a una velocidad lo suficientemente alta. A velocidades de bits asintóticamente alto, cortando el paso tamaño en media aumenta la tasa de bits por aproximadamente 1 bits por muestra (porque se necesita 1 bit para indicar si el valor está en la mitad izquierda o derecha del intervalo previo de tamaño doble) y reduce el error cuadrado medio por un factor de 4 (es decir, 6 dB) basado en el  aproximación.
aproximación.
A velocidades de bits asintóticamente alto, la aproximación de 6 dB/bit es compatible con muchos archivos PDF fuente por riguroso análisis teórico.[4][5][7][8] Por otra parte, la estructura de la óptima cuantificador escalar (en el sentido de ritmo – distorsión) acerca de un cuantificador uniforme bajo estas condiciones.[7][8]
Otros campos
En realidad son quantized muchas cantidades físicas por entidades físicas. Ejemplos de campos donde se aplica esta limitación electrónica (debido a los electrones), óptica (debido a los fotones), Biología (debido a ADN), y química (debido a moléculas). Esto es conocido como el "límite de ruido cuántico" de sistemas en esos campos. Esto es una manifestación diferente de "error del quantization", en el cual los modelos teóricos pueden ser análogos pero físicamente se produce digitalmente. Alrededor de la límite cuántico, desaparece la distinción entre las cantidades analógicas y digitales.[citación necesitada]
Véase también
- Codificador de beta
- Resolución de bits
- Error de discretización
- Posterización
- Modulación por impulsos codificados
- Dilución de regresión -un sesgo en el parámetro estima debidos a errores como cuantización en la variable independiente o explicativa
Notas
- ^ Hodgson, Jay (2010). Comprensión Records, p.56. ISBN 978-1-4411-5607-5. Adaptado de Franz, David (2004). Grabación y producción en el estudio casero, p 38-9. Berklee Press.
- ^ Allen Gersho y Robert M. Gray, Vector Quantization y compresión de señal, Springer, ISBN 978-0-7923-9181-41991.
- ^ William Fleetwood Sheppard, "En el cálculo de los valores más probables de frecuencia constantes de datos dispuestos según divisiones equidistantes de una escala", Actas de la sociedad matemática de LondresVol. 29, pp. 353 – 80, 1898.Doi:10.1112/PLMS/S1-29.1.353
- ^ a b c d R. w el. Bennett "Espectros de señales Quantized", Campana sistema Technical JournalVol. 27, pp. 446 – 472, de julio de 1948.
- ^ a b B. M. Oliver, J. R. Pierce, y Claude E. Shannon, "La filosofía del PCM", Actas de la iraVol. 36, pp. 1324 – 1331, noviembre de 1948. Doi:10.1109/JRPROC.1948.231941
- ^ Seymour Stein y J. Jay Jones, Principios de la comunicación moderna, McGraw-Hill, ISBN 978-0-07-061003-31967 (pág. 196).
- ^ a b c Herbert Gish y John N. Pierce, "cuantizar asintóticamente eficiente", IEEE Transactions on teoría de la informaciónIT vol.-14, nº 5, pp. 676 – 683, septiembre de 1968. Doi:10.1109/TIT.1968.1054193
- ^ a b c d e f g h Robert M. Gray y David L. Neuhoff, "Quantization", IEEE Transactions on teoría de la informaciónIT vol.-44, Nº 6, pp. 2325 – 2383, octubre de 1998. Doi:10.1109/18.720541
- ^ a b Allen Gersho, "Quantization", Revista IEEE Communications Society, págs. 16 – 28, septiembre de 1977. Doi:10.1109/MCOM.1977.1089500
- ^ Bernard Widrow, "Un estudio de cuantificación difícil amplitud por medio de la teoría de muestreo de Nyquist", Teoría de circuitos de transporte iraVol. CT-3, págs. 266 – 276, 1956. Doi:10.1109/TCT.1956.1086334
- ^ a b c Bernard Widrow, "Análisis estadístico de amplitud quantized muestreados sistemas de datos", AIEE trans. pt. II: IND LIQ.Vol. 79, págs. 555 – 568, enero de 1961.
- ^ Daniel Marco y David L. Neuhoff, "La validez del modelo de ruido aditivo para uniformes Quantizers escalares", IEEE Transactions on teoría de la informaciónVol. IT-51, núm. 5, págs. 1739 – 1755, mayo de 2005. Doi:10.1109/TIT.2005.846397
- ^ Pohlman, Ken C. (1989). Principios de Audio Digital 2ª edición. SAMS. p. 60.
- ^ Okelloto, Tom (2001). El arte del Audio Digital 3ª edición. Focal Press. ISBN0-240-51587-0.
- ^ Nariman Farvardin y James W. Modestino, "Quantizer óptimo funcionamiento para una clase de fuentes sin memoria no-Gaussian", IEEE Transactions on teoría de la informaciónVol. IT-30, núm. 3, págs. 485 – 497, mayo de 1982 (sección VI.C y Apéndice B). Doi:10.1109/TIT.1984.1056920
- ^ a b Gary J. Sullivan, "Eficiente cuantización escalar de exponencial y Variables aleatorias laplaciano", IEEE Transactions on teoría de la informaciónVol. IT-42, nº 5, págs. 1365 – 1374, septiembre de 1996. Doi:10.1109/18.532878
- ^ Toby Berger, "Quantizers óptimo y permutación códigos", IEEE Transactions on teoría de la informaciónVol. IT-18, Nº 6, pp. 759 – 765, noviembre de 1972. Doi:10.1109/TIT.1972.1054906
- ^ Toby Berger, "Quantizers mínima de la entropía y permutación códigos", IEEE Transactions on teoría de la informaciónVol. IT-28, Nº 2, pp. 149-157, marzo de 1982. Doi:10.1109/TIT.1982.1056456
- ^ Stuart P. Lloyd, "Least Squares Quantization en PCM", IEEE Transactions on teoría de la informaciónVol. IT-28, págs. 129-137, Nº 2, marzo de 1982 Doi:10.1109/TIT.1982.1056489 (documentado en un manuscrito para recabar observaciones en el trabajo Laboratorios Bell con una fecha de registro del Departamento de 31 julio de 1957 y también presentada en la reunión de 1957 de la Instituto de estadística matemáticaAunque no formalmente publicados hasta 1982).
- ^ Joel máximo, "cuantificar para distorsión mínima", Transacciones de ira en la teoría de la informaciónVol. IT-6, pp. 7 – 12 de marzo de 1960. Doi:10.1109/TIT.1960.1057548
- ^ Philip A. Chou, Tom Lookabaugh, y Robert M. Gray, "Con restricciones de entropía Vector Quantization", IEEE Transactions on Acoustics, discurso y procesamiento de señalesVol. ASSP-37, no. 1, enero de 1989. Doi:10.1109/29.17498
Referencias
- Sayood, Khalid (2005), Introducción a la compresión de datos, tercera ediciónMorgan Kaufmann, ISBN978-0-12-620862-7
- Jayant, Nikil S.; Noll, Peter (1984), La codificación digital de formas de onda: principios y aplicaciones de voz y VideoPrentice-Hall, ISBN978-0-13-211913-9
- Gregg, David W. (1977), Comunicación Digital y analógicaJohn Wiley, ISBN978-0-471-32661-8
- Stein, Seymour; Jones, J. Jay (1967), Principios de la comunicación moderna, McGraw-Hill, ISBN978-0-07-061003-3
Enlaces externos
- Ruido de cuantización en Computación Digital, procesamiento de señales y ControlBernard Widrow y István Kollár, 2007.
- La relación de rango dinámico para tamaño de palabra de datos en el procesamiento de Audio Digital
- Redondear la varianza Error — derivación de potencia de ruido de q²/12 por error de redondeo
- Evaluación dinámica de convertidores D/a de alta velocidad, alta resolución Esboza medidas HD, IMD y NPR, incluye también una derivación del ruido de cuantización
- Señal a ruido de cuantización en quantized sinusoidal
|
||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
Otras Páginas
- Gota
- Frank Bliss (jugadores de Milwaukee grises de categoria)
- Palm Centro
- Conectar reproductor
- POU3F1
- Encriptacion basada en certificados
- Calcis, Alabama
- Sisseton Wahpeton Oyate
- Gossypiboma
- Ciclo de negocio
- Adcon-L
- George Chapman (curador)
- Francia seleccion femenina de futbol sub-17
- Liam Fontaine
- Izvor
- Propria de la lamina
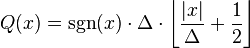 ,
,
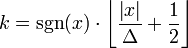 ,
,
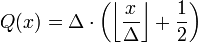 ,
,

 .
.
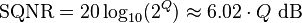


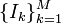 , definiendo
, definiendo 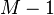 límite (decisión) valores
límite (decisión) valores 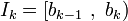 para
para 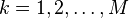 , con los límites extremos definidos por
, con los límites extremos definidos por  y
y  . Todas las entradas
. Todas las entradas 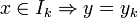 .
.![p_k = P[x \in I_k] = \int_{b_{k-1}}^{b_k} f(x)dx](http://upload.wikimedia.org/math/9/1/8/91861058256271d87464b9931c3b9a58.png) .
.
 .
.
![D = E[(x-Q(x))^2] = \int_{-\infty}^{\infty} (x-Q(x))^2f(x)dx = \sum_{k=1}^{M} \int_{b_{k-1}}^{b_k} (x-y_k)^2 f(x)dx](http://upload.wikimedia.org/math/4/9/e/49ee960cd614cd3180061b198772dd46.png) .
.
 , reducir la tasa de bits
, reducir la tasa de bits  , minimizar la distorsión
, minimizar la distorsión 

 .
.

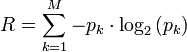 .
.
![D=E[(x-Q(x))^2] = \int_{-\infty}^{\infty} (x-Q(x))^2f(x)dx = \sum_{k=1}^{M} \int_{b_{k-1}}^{b_k} (x-y_k)^2 f(x)dx =\sum_{k=1}^{M} d_k](http://upload.wikimedia.org/math/6/a/8/6a8715dfbc9eec977dcfd8981dea45f6.png) .
.
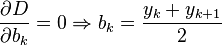 ,
,

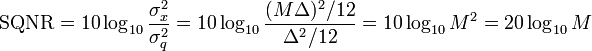 .
.