Medida del riesgo de distorsión
|
|
Este artículo proporciona contexto insuficiente para aquellos no familiarizados con el tema. (Mayo de 2012) |
En matemáticas financieras, un medida del riesgo de distorsión es un tipo de medida del riesgo que se relaciona con la función de distribución acumulativa de la retorno de un cartera financiera.
Contenido
- 1 Definición matemática
- 1.1 Propiedades
- 2 Ejemplos
- 3 Véase también
- 4 Referencias
Definición matemática
La función 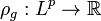 asociado con el función de distorsión
asociado con el función de distorsión ![g: [0,1] \to [0,1]](http://upload.wikimedia.org/math/9/7/f/97fd26d67e9595db275d4a69efc1fd5b.png) es un medida del riesgo de distorsión Si lo haces por cualquier variable aleatoria de ganancias
es un medida del riesgo de distorsión Si lo haces por cualquier variable aleatoria de ganancias  (donde
(donde 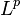 es el Lp espacio) entonces
es el Lp espacio) entonces
donde  es la función de distribución acumulativa para
es la función de distribución acumulativa para  y
y  es la función de distorsión dual
es la función de distorsión dual  .[1]
.[1]
If  casi con toda seguridad Entonces
casi con toda seguridad Entonces  está dada por la Choquet integral, es decir,
está dada por la Choquet integral, es decir,  [1][2] Equivalente,
[1][2] Equivalente, ![\rho_g(X) = \mathbb{E}^{\mathbb{Q}}[-X]](http://upload.wikimedia.org/math/f/e/d/fed48379d0bf8034811a644153174ab5.png) [2] tal que
[2] tal que  es el medida de la probabilidad generado por
es el medida de la probabilidad generado por  , es decir, para cualquier
, es decir, para cualquier 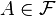 el Sigma-álgebra Entonces
el Sigma-álgebra Entonces  .[3]
.[3]
Propiedades
Además de las propiedades de las medidas de riesgo general, también tienen medidas de riesgo de distorsión:
- Invariante de ley:: If la distribución de
 y
y  son el mismo entonces
son el mismo entonces 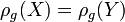 .
. - Monotono con respecto a la primera orden dominancia estocástica.
- If
 es un cóncavo función de distorsión, entonces
es un cóncavo función de distorsión, entonces  Es monótona con respecto a la dominancia estocástica de segundo orden.
Es monótona con respecto a la dominancia estocástica de segundo orden.
- If
 es un cóncavo distorsión de la función si y sólo si
es un cóncavo distorsión de la función si y sólo si  es un medida de riesgo coherente.[1][2]
es un medida de riesgo coherente.[1][2]
Ejemplos
- Valor en riesgo es una medida de riesgo de distorsión con función de distorsión asociada
 [2][3]
[2][3] - Valor condicional en riesgo es una medida de riesgo de distorsión con función de distorsión asociada
 [2][3]
[2][3] - La negativa expectativa es una medida de riesgo de distorsión con función de distorsión asociada
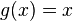 .[1]
.[1]
Véase también
- Medida del riesgo
- Medida de riesgo coherente
- Medida del riesgo de desviación
- Medida del riesgo espectral
Referencias
- ^ a b c d Sereda, E. N.; BRONSHTEIN, E. M.; Rachev, S. T.; Fabozzi, F. J.; Sol, w el.; Stoyanov, S. V. (2010). "Medidas de riesgo de distorsión en la optimización de la cartera". "Manual de construcción de cartera". p. 649. Doi:10.1007/978-0-387-77439-8_25. ISBN978-0-387-77438-1.
- ^ a b c d e Julia L. Wirch; Mary R. Hardy. "Las medidas de riesgo de distorsión: coherencia y dominio estocástico" (pdf). 10 de marzo de 2012.
- ^ a b c Balbás, A.; Garrido, J.; Mayoral, S. (2008). "Propiedades de las medidas de riesgo de distorsión". Metodología y cálculo de probabilidad aplicada 11 (3): 385. Doi:10.1007/s11009-008-9089-z.
- Wu, Xianyi; Xian Zhou (07 de abril de 2006). "Una nueva caracterización de las primas de distorsión vía aditividad contable para los riesgos del comonotonic". Seguros: Matemáticas y economía 38 (2): 324 – 334. Doi:10.1016/j.insmatheco.2005.09.002. 14 de marzo de 2012.

 y
y  son el mismo entonces
son el mismo entonces 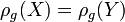 .
.

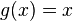 .
.