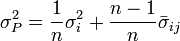Diversificación (finanzas)
| Finanzas |
|---|
 |
|
Mercados financieros
|
|
Instrumentos financieros
|
|
Finanzas corporativas
|
|
Finanzas personales
|
|
Finanzas públicas
|
|
Bancos y banca
|
|
Regulación financiera
|
|
Estándares
|
|
Historia económica
|
En finanzas, diversificación significa reducir no sistemática riesgo por invertir en una variedad de activos. Si el valor de los activos no se mueven hacia arriba y hacia abajo en perfecta sincronía, un diversificado cartera tendrá menos riesgo que los promedio ponderado riesgo de sus constituyentes activos y a menudo menos riesgo que la menos arriesgada de su constituyente.[1]
La diversificación es uno de los dos técnicas generales para reducir el riesgo de inversión. El otro es cobertura. La diversificación se basa en la falta de una fuerte relación positiva entre los rendimientos de los activos, y funciona incluso cuando correlaciones son cerca de cero o algo positivo. Cobertura se basa en la correlación negativa entre los activos, o cortocircuito activos con correlación positiva.
Contenido
- 1 Ejemplos
- 2 Expectativas de retorno mientras diversificando
- 3 Máxima diversificación
- 4 Efecto de la diversificación de la varianza
- 5 Riesgos diversificables y no diversificables
- 6 Un ejemplo empírico relativa diversificación a la reducción del riesgo
- 7 Estrategias de diversificación empresarial
- 8 Historia
- 9 Diversificación con una cartera igualmente ponderada
- 10 Véase también
- 11 Notas
- 12 Referencias
- 13 Enlaces externos
Ejemplos
El ejemplo más simple de la diversificación es proporcionado por el proverbio"No poner todos los huevos en una canasta". Bajando la cesta se romperán todos los huevos. Colocar cada huevo en una cesta diferente es más diversificada. Hay más riesgo de perder un huevo, pero reduce el riesgo de perder todo de ellos.
En finanzas, un ejemplo de una cartera diversificada es mantener un único stock. Esto es arriesgado; No es inusual para una sola población que bajar un 50% en un año. Es mucho menos común que una cartera de 20 acciones bajar mucho, sobre todo si se seleccionan al azar. Si las existencias se seleccionan de una variedad de industrias, tamaños y tipos (por ejemplo, algunos acciones de crecimiento y algunos acciones de valor) es aún menos probable.
Desde mediados de 1970, se también ha afirmado que la diversificación geográfica podría generar retornos ajustados por riesgo superiores para grandes inversores institucionales reduciendo el riesgo total de la cartera mientras captura algunas de las más altas tasas de rendimiento ofrecidos por el mercados emergentes de Asia y América Latina.[2][3]
Expectativas de retorno mientras diversificando
Si el previo expectativas de los rendimientos de todos los activos de la cartera son idénticos, el retorno esperado en una cartera diversificada será idéntica a la de una cartera diversificada. Ex post, algunos activos hará mejor que otros; Pero puesto que no se sabe de antemano qué activos funcionará mejor, este hecho no puede ser explotada por adelantado. El ex post retorno sobre una cartera diversificada no puede superar la inversión de alto rendimiento y de hecho siempre será menor que el retorno más alto (a menos que todas las devoluciones están ex post idéntico). Por el contrario, la rentabilidad de la cartera diversificada siempre será mayor que el de la inversión de peores resultados. Así que diversificando, uno pierde la oportunidad de tener invertidos exclusivamente en el único activo que sale mejor, pero también uno evita tener invertidos exclusivamente en el activo que sale peor. Es el papel de diversificación: reduce la gama de los posibles resultados. Diversificación necesita no ayudar o lastimar las ganancias esperadas, a menos que la alternativa no diversificada cartera tiene una mayor rentabilidad esperada.[4]
Máxima diversificación
Habida cuenta de las ventajas de la diversificación, muchos expertos[¿Quién?] Recomendamos la máxima diversificación, también conocido como "comprar el cartera de mercado.” Por desgracia, no es sencillo identificar esa cartera. La primera definición proviene de la modelo de precios de activos de capital que sostiene la máxima diversificación viene comprando un prorrata participación de todos los activos. Esta es la idea subyacente fondos de índice.
Diversificación no tiene ningún máximo. Todos los activos correlacionados, igualmente ponderado agregado a una cartera pueden agregar a esa diversificación de carteras medidos. Cuando los activos no están correlacionados uniformemente, un método de ponderación que pone activos en proporción a su correlación relativa puede maximizar la diversificación disponible.
"El riesgo de paridad" es una idea alternativa. Esto pesos activos inversamente proporcional a riesgo, por lo que la cartera tiene igual riesgo en todas las clases de activos. Esto se justifica tanto por razones teóricas y con el argumento pragmático de que riesgo futuro es mucho más fácil de predecir que el valor de mercado de futuro o huella económica futura. "Correlación paridad" es una extensión de paridad de riesgo y es la solución mediante el cual cada activos en una cartera tiene una correlación con la cartera de igualdad y por lo tanto es el "más diversificado portafolio". Paridad de riesgo es el caso especial de paridad correlación cuando todas las correlaciones pares son iguales.[5]
Efecto de la diversificación de la varianza
Una simple medida de riesgo financiero es varianza. La diversificación puede reducir la varianza del retorno de un portafolio por debajo de lo que sería si toda la cartera se invirtieron en el activo con la menor variación de vuelta, incluso si los retornos de los activos no están correlacionados. Por ejemplo, activos que X tener retorno estocástico  y activos Y retorno estocástico
y activos Y retorno estocástico  , con respectivas varianzas retorno
, con respectivas varianzas retorno  y
y  . Si la fracción
. Si la fracción  de una cartera de una unidad (por ejemplo uno millones de dólares) está situada en activo X y la fracción
de una cartera de una unidad (por ejemplo uno millones de dólares) está situada en activo X y la fracción 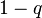 se coloca en Y, la cartera estocástica de retorno es
se coloca en Y, la cartera estocástica de retorno es  . If
. If  y
y  están correlacionados, la variación de la cartera de retorno es
están correlacionados, la variación de la cartera de retorno es  . El valor de la varianza, minimizando
. El valor de la varianza, minimizando  es
es ![q=\sigma^{2}_y/[\sigma^{2}_x+\sigma^{2}_y]](http://upload.wikimedia.org/math/7/5/4/7544d6614f3b9bb711699f2ccbfc6f0b.png) , que es estrictamente entre
, que es estrictamente entre  y
y  . Utilizando este valor de
. Utilizando este valor de  en la expresión de la varianza del portafolio retorno da el último como
en la expresión de la varianza del portafolio retorno da el último como ![\sigma^{2}_x\sigma^{2}_y/[\sigma^{2}_x+\sigma^{2}_y]](http://upload.wikimedia.org/math/5/2/e/52e5c132834fc4fd9b5511f509d207d1.png) , que es menos de lo que sería en cualquiera de los valores diversificados
, que es menos de lo que sería en cualquiera de los valores diversificados 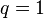 y
y 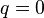 (que respectivamente dan una variación retorno cartera de
(que respectivamente dan una variación retorno cartera de  y
y  ). Tenga en cuenta que el efecto favorable de la diversificación en varianza portafolio aumentaría si
). Tenga en cuenta que el efecto favorable de la diversificación en varianza portafolio aumentaría si  y
y  se correlacionaron negativamente pero disminuye (aunque no necesariamente eliminado) si ellos se correlacionaron positivamente.
se correlacionaron negativamente pero disminuye (aunque no necesariamente eliminado) si ellos se correlacionaron positivamente.
En general, la presencia de los más activos en una cartera conduce a mayores beneficios de la diversificación, como puede verse por teniendo en cuenta la varianza portafolio en función de  , el número de activos. Por ejemplo, si devuelve todos los activos no está correlacionados mutuamente y tiene varianzas iguales
, el número de activos. Por ejemplo, si devuelve todos los activos no está correlacionados mutuamente y tiene varianzas iguales  , cartera varianza se minimiza mediante la celebración de todos los activos en las proporciones iguales
, cartera varianza se minimiza mediante la celebración de todos los activos en las proporciones iguales  .[6] Entonces es igual la varianza del retorno de la cartera
.[6] Entonces es igual la varianza del retorno de la cartera ![var[(1/n)x_{1}+(1/n)x_{2}+...+(1/n)x_{n}]](http://upload.wikimedia.org/math/5/c/9/5c98cf0a71503689f0e32b084d38fa1c.png) =
=  =
=  , que es Monótonamente decreciente en
, que es Monótonamente decreciente en  .
.
Este último análisis pueden ser adaptado para mostrar por qué Agregar activos riesgosos no correlacionados a una cartera,[7][8] aumentando de tamaño de la cartera, no es la diversificación, que consiste en dividir la cartera entre muchas pequeñas inversiones. En el caso de agregar las inversiones, la rentabilidad de la cartera es  En lugar de
En lugar de  y es la varianza del retorno cartera si los activos no están correlacionados
y es la varianza del retorno cartera si los activos no están correlacionados ![var[x_1+x_2+\dots +x_n] = \sigma^{2}_{x} + \sigma^{2}_{x}+ \dots + \sigma^{2}_{x} = n\sigma^{2}_{x},](http://upload.wikimedia.org/math/0/2/3/02336dd7b5dbb3595276c4557ca6c252.png) ¿Cuál es aumento en n en lugar de disminuir. Así, por ejemplo, cuando una compañía de seguros agrega políticas más correlacionadas a su cartera, esta expansión no se representa la diversificación — la diversificación se produce en la difusión de los riesgos de la compañía de seguros sobre un gran número de propietarios de parte de la empresa.
¿Cuál es aumento en n en lugar de disminuir. Así, por ejemplo, cuando una compañía de seguros agrega políticas más correlacionadas a su cartera, esta expansión no se representa la diversificación — la diversificación se produce en la difusión de los riesgos de la compañía de seguros sobre un gran número de propietarios de parte de la empresa.
Riesgos diversificables y no diversificables
El modelo de precios de activos de capital introdujo los conceptos de riesgos diversificables y no diversificables. Son sinónimos para riesgos diversificables riesgos idiosincrásicos, riesgo asistemático y riesgo específica de la seguridad. Son sinónimos para riesgos no diversificables riesgo sistemático, Beta riesgo y riesgo de mercado.
Si uno compra todas las acciones el S & P 500 Obviamente uno se expone sólo a los movimientos en Índice. Si uno compra una sola población en el S & P 500, uno está expuesto a los movimientos del índice y los movimientos en el stock basado en su empresa subyacente. El primer riesgo se llama "no diversificables," porque existe sin embargo muchas S & P 500 acciones son compradas. El segundo riesgo se llama "diversificables", porque puede ser reducido por la diversificación entre las poblaciones.
Tenga en cuenta que también existe el riesgo de overdiversifying a tal punto que sufrirá su rendimiento y va a terminar pagando mayormente por honorarios.
El capital activo precios modelo sostiene que los inversionistas sólo deben ser compensados por riesgos no diversificables. Otros modelos financieros permiten múltiples fuentes de riesgos no diversificables, pero también insisten en que riesgos diversificables no deben llevar cualquier retorno más esperado. Todavía otros modelos no aceptan esta contención[9]
Un ejemplo empírico relativa diversificación a la reducción del riesgo
En 1977 Elton y Gruber[10] resultó un ejemplo empírico de los beneficios de diversificación. Su enfoque fue considerar una población de 3290 títulos disponibles para su posible inclusión en una cartera y considerar el riesgo promedio sobre todas las posibles elegidas al azar n-carteras de activos con cantidades iguales celebrada en cada activo incluido, para varios valores de n. Sus resultados se resumen en la tabla siguiente. Puede verse que la mayoría de los beneficios de diversificación vienen para n≤30.
| Número de acciones en cartera | Promedio desviación estándar de los retornos de cartera | Relación de cartera de desviación a la desviación estándar de una sola población |
|---|---|---|
| 1 | 49,24% | 1.00 |
| 2 | 37,36 | 0.76 |
| 4 | 29,69 | 0.60 |
| 6 | 26,64 | 0,54 |
| 8 | 24,98 | 0.51 |
| 10 | 23,93 | 0.49 |
| 20 | 21,68 | 0.44 |
| 30 | 20,87 | 0.42 |
| 40 | 20,46 | 0.42 |
| 50 | 20,20 | 0,41 |
| 400 | 19,29 | 0.39 |
| 500 | 19,27 | 0.39 |
| 1000 | 19,21 | 0.39 |
Estrategias de diversificación empresarial
En los modelos de cartera corporativa, la diversificación es considerada como ser vertical u horizontal. Diversificación horizontal es considerada como una línea de productos en expansión o adquiriendo empresas relacionadas. Diversificación vertical es sinónima de integración de la cadena de suministro o amalgamando canales de distribución.
Non-incremental diversificación es una estrategia seguida por conglomerados, donde las líneas de negocio individuales tienen poco que ver uno con el otro, sin embargo, la empresa es lograr la diversificación de los factores de riesgo exógenos para estabilizar y dar oportunidad a la administración activa de diversos recursos.
Historia
La diversificación es mencionada en el Biblia, en el libro de Eclesiastés que fue escrita en aproximadamente 935 A.C.:[11]
- Pero dividir sus inversiones entre muchos lugares,
- para ti no sé qué riesgos pueden delante. [12]
La diversificación también es mencionada en el Talmud. Dado que la fórmula es dividir los bienes en tercios: un tercio en los negocios (comprar y vender cosas), un tercio mantiene líquido (monedas de oro por ejemplo) y un tercio en tierra (Inmobiliaria).
La diversificación es mencionada en Shakespeare[13] (Mercader de Venecia):
- Mis empresas no están en un fondo de confianza,
- Ni a un solo lugar; Tampoco es mi finca toda
- Sobre la fortuna de este presente año:
- Por lo tanto, mi mercancía me entristece no.
La comprensión moderna de se remonta a la obra de diversificación Harry Markowitz[14] en la década de 1950.
Diversificación con una cartera igualmente ponderada
El retorno esperado de un portafolio es un promedio ponderado de los rendimientos esperados de cada activo individual:
donde  es la proporción de la riqueza invertida total del inversionista en activos
es la proporción de la riqueza invertida total del inversionista en activos  .
.
La varianza del retorno del portafolio viene dada por:
Insertar en la expresión para ![\mathbb{E}[R_P]](http://upload.wikimedia.org/math/c/3/a/c3ae12d6dadb7e3ef003e47726ad2ffb.png) :
:
Arreglos:
donde 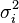 es la varianza en activo
es la varianza en activo  y
y 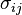 es la covarianza entre activos
es la covarianza entre activos  y
y  . En una cartera igualmente ponderada,
. En una cartera igualmente ponderada,  .
.
La varianza del portafolio entonces se convierte en:
Donde  es el promedio de las covarianzas
es el promedio de las covarianzas 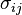 para
para  . Simplificando obtenemos
. Simplificando obtenemos
A medida que crece el número de activos obtenemos la fórmula asintótica:
Así, en una cartera igualmente ponderada, la varianza del portafolio tiende a la media de covarianzas entre valores como el número de valores se convierte arbitrariamente grande.
Véase también

- Teorema de límite central
- Medida de riesgo coherente
- Dollar cost averaging
- Correlación financiera
- Lista de temas de finanzas
- Teoría moderna de portafolio
- Riesgo sistemático
Notas
- ^ Sullivan, Arthur; Steven M. Sheffrin (2003). Economía: Principios en acción. Upper Saddle River, NJ 07458: Pearson Prentice Hall. p. 273. ISBN0-13-063085-3.
- ^ (Francés) "ver a Nicolas M. J. Firzli,"Asia-Pacific fondos como diversificación herramientas para los inversores institucionales", Revue analizar Financière/The francés sociedad de financiera analistas (SFAF)". 2009-04-02
- ^ (Inglés) "ver a Michael Prahl,"Asia Private Equity – entregará su promesa?", INSEAD Global Private Equity iniciativa (GPEI)". 2011-06-15
- ^ Goetzmann, William N. Una introducción a la teoría de inversión. II. carteras de activos. Recuperado encendido 20 de noviembre de 2008.
- ^ Asness, acantilado; David Kabiller y Michael Mendelson Uso de derivados y el apalancamiento para mejorar el desempeño de la cartera, Institutional Investor, 13 de mayo de 2010. Recuperado encendido 21 de junio de 2010.
- ^ Samuelson, Paul, "General prueba que la diversificación paga"Diario financiero y análisis cuantitativo 2, marzo de 1967, 1-13.
- ^ Samuelson, Paul, "riesgo y la incertidumbre: una falacia de números grandes," Scientia 98, 1963, 108-113.
- ^ Ross, Stephen, "agregando los riesgos: la falacia de Samuelson de grandes números revisitados," Diario financiero y análisis cuantitativo 34, septiembre de 1999, 323-339.
- ^ .Fama, Eugene F.; Merton H. Miller (junio de 1972). La teoría de las finanzas. Holt Rinehart & Winston. ISBN978-0-15-504266-7.
- ^ E. Elton J. y M. J. Gruber, "el riesgo de reducción y tamaño de cartera: una solución analítica," Journal of Business 50 (octubre de 1977), págs. 415-37
- ^ Biblia de estudio de aplicación de la vida: Nueva traducción viviente. Wheaton, Illinois: Tyndale House Publishers, Inc. 1996. p. 1024. ISBN0-8423-3267-7.
- ^ Eclesiastés 11:2 RVR
- ^ La única guía para una estrategia de inversión ganadora que necesitará
- ^ Markowitz, Harry M. (1952). "Selección de cartera". Revista de finanzas 7 (1): 77-91. Doi:10.2307/2975974. JSTOR2975974.
Referencias
- James Lorie, Peter Dodd y Mary Kimpton, El mercado de valores: Teorías y pruebas (2do edn 1985) 85, mayor valor de diversificación viene de las primeros 15 o 20 acciones diferentes en una cartera
Enlaces externos
- Análisis de macro-inversiones, Prof. William Sharpe F., La Universidad de Stanford
- Diversificador de carteraCarteras diversificadas dinámicamente generados
- Correlaciones de activosGeneradas dinámicamente las matrices de correlación para las clases principales de activos
- Una introducción a la teoría de inversiónProf. William N. Goetzmann, Yale School of Management
- Resumen de futuros gestionados
- Cartera diversificada sintético basado en la optimización de media varianza,
- 4 ejemplos de pozo retiro carteras diversificadas,
- Diversificación de la cartera,
|
||||||||||||||||||||||||||||||||||||
Otras Páginas
- LIO (destino SCSI)
- USAA (redireccion de Unidos servicios Auto Assoc)
- Esta es Anita
- Salud procedimiento comun sistema de codificacion
- Motor Volkswagen G60
- Nissan MA10ET
- Modelo de referencia de seguridad de la informacion y la seguridad
- H. Robert Fowler
- Internet Marketing Conference
- Lista de motores de Auto Skoda
- Dick Callen House
- Terry Keel (alumnos de la Universidad de Houston de categoria)
![\mathbb{E}[R_P] = \sum^{n}_{i=1}x_i\mathbb{E}[R_i]](http://upload.wikimedia.org/math/b/2/4/b249b05aef63e1eb81204af99d007a61.png)
![\underbrace{\text{Var}(R_P)}_{\equiv \sigma^{2}_{P}} = \mathbb{E}[R_P - \mathbb{E}[R_P]]^2](http://upload.wikimedia.org/math/b/c/1/bc133569410c93ae00a5a5f983e35035.png)
![\sigma^{2}_{P} = \mathbb{E}\left[\sum^{n}_{i=1}x_i R_i - \sum^{n}_{i=1}x_i\mathbb{E}[R_i]\right]^2](http://upload.wikimedia.org/math/c/6/0/c602c0edb60cf8c85b30909701da43b1.png)
![\sigma^{2}_{P} = \mathbb{E}\left[\sum^{n}_{i=1}x_i(R_i - \mathbb{E}[R_i])\right]^2](http://upload.wikimedia.org/math/8/f/6/8f64ccb4650d765bd0ccea47ac8acfff.png)
![\sigma^{2}_{P} = \mathbb{E}\left[\sum^{n}_{i=1} \sum^{n}_{j=1} x_i x_j(R_i - \mathbb{E}[R_i])(R_j - \mathbb{E}[R_j])\right]](http://upload.wikimedia.org/math/4/b/3/4b3227f97f3db53e43321a5a8845e0f1.png)
![\sigma_{P}^{2}=\mathbb{E}\left[\sum_{i=1}^{n}x_{i}^{2}(R_{i}-\mathbb{E}[R_{i}])^{2}+\sum_{i=1}^{n}\sum_{j=1,i\neq j}^{n}x_{i}x_{j}(R_{i}-\mathbb{E}[R_{i}])(R_{j}-\mathbb{E}[R_{j}])\right]](http://upload.wikimedia.org/math/9/f/6/9f60b328d56b7e5fe1f92005c5710b15.png)
![\sigma_{P}^{2}=\sum_{i=1}^{n}x_{i}^{2}\underbrace{\mathbb{E}\left[R_{i}-\mathbb{E}[R_{i}]\right]^{2}}_{\equiv\sigma_{i}^{2}}+\sum_{i=1}^{n}\sum_{j=1,i\neq j}^{n}x_{i}x_{j}\underbrace{\mathbb{E}\left[(R_{i}-\mathbb{E}[R_{i}])(R_{j}-\mathbb{E}[R_{j}])\right]}_{\equiv\sigma_{ij}}](http://upload.wikimedia.org/math/b/e/0/be09603a54c0fd67cf65e4c6f7306292.png)