Medida de riesgo coherente
|
|
Se ha sugerido que esta sección sea combinado con Medida de riesgo coherente y Función de distorsión. (Discutir) Propuso desde enero de 2014. |
|
|
Este artículo también puede ser técnica para la mayoría de los lectores a entender. (Agosto de 2013) |
En el campo de economía financiera Hay un número de maneras que el riesgo puede definirse; aclarar el concepto teóricos han descrito una serie de propiedades que un medida del riesgo podría o no podría tener. A medida de riesgo coherente es una función  satisface las propiedades de moniticidad, Sub-aditividad, homogeneidad, y invariancia translacional.
satisface las propiedades de moniticidad, Sub-aditividad, homogeneidad, y invariancia translacional.
Contenido
- 1 Propiedades
- 1.1 Medidas de riesgo convexo
- 2 Marco general de transformación de Wang
- 3 Ejemplos de medida de riesgo
- 3.1 Valor en riesgo
- 3.2 Promedio del valor en riesgo
- 3.3 Entrópico valor en riesgo
- 3.4 Cola de valor en riesgo
- 3.5 Medida proporcional del riesgo peligro (PH)
- 3.6 medidas de riesgo g-entrópico
- 3.7 La medida del riesgo Wang
- 3.8 Medida del riesgo entrópica
- 3.9 Precio Superhedging
- 4 Conjunto de valores
- 4.1 Propiedades
- 4.2 Medida del valor conjunto convexo riesgo
- 5 Representación doble
- 6 Véase también
- 7 Referencias
- 8 Enlaces externos
Propiedades
Considerar un resultado aleatorio  visto como un elemento de un espacio lineal
visto como un elemento de un espacio lineal  de funciones medibles, definidos en un espacio probabilístico apropiado. A funcional
de funciones medibles, definidos en un espacio probabilístico apropiado. A funcional 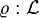 →
→ 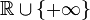 se dice que es medida de riesgo coherente para
se dice que es medida de riesgo coherente para  si satisface las siguientes propiedades:[1]
si satisface las siguientes propiedades:[1]
- Normalizado
-

Es decir, el riesgo de no mantener activos es cero.
- Moniticidad
-
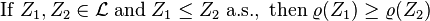
Es decir, si portfolio 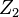 siempre tiene mejores valores de cartera
siempre tiene mejores valores de cartera 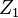 bajo casi todos escenarios entonces el riesgo de
bajo casi todos escenarios entonces el riesgo de 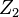 debe ser menor que el riesgo de
debe ser menor que el riesgo de 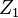 .[2] Por ejemplo si
.[2] Por ejemplo si 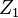 es un dinero llamar opción (o no) en una acción, y
es un dinero llamar opción (o no) en una acción, y 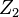 es también un dinero llamar opción con un precio más bajo de la huelga.
es también un dinero llamar opción con un precio más bajo de la huelga.
- Sub-aditividad
-

De hecho, el riesgo de dos carteras juntos puedes peor que sumando por separado los dos riesgos: es la diversificación principio.
- Homogeneidad positiva
-
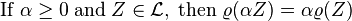
Hablando libremente, si el doble su cartera y luego doble el riesgo.
- Invariancia de traducción
If  es una cartera determinista con retorno garantizado
es una cartera determinista con retorno garantizado  y
y  Entonces
Entonces
La cartera  es sólo la adición de efectivo
es sólo la adición de efectivo  a su cartera
a su cartera  . En particular, si
. En particular, si  Entonces
Entonces  .
.
Medidas de riesgo convexo
La noción de coherencia se ha relajado posteriormente. De hecho, las nociones de Sub-aditividad y homogeneidad positiva pueden ser sustituidas por la noción de convexidad:[3]
- Convexidad
-
![If \ Z_1,Z_2 \in \mathcal{L}\text{ and }\lambda \in [0,1] \text{ then }\varrho(\lambda Z_1 + (1-\lambda) Z_2) \leq \lambda \varrho(Z_1) + (1-\lambda) \varrho(Z_2)](//upload.wikimedia.org/math/9/7/7/9776e40f411fa860810a0706d7b326f3.png)
Marco general de transformación de Wang
- Wang transformación de la función de distribución decumulative
Una transformación de la función de distribución decumulative de Wang es una función creciente ![g \colon [0,1] \rightarrow [0,1]](http://upload.wikimedia.org/math/1/c/5/1c5daa33c649dd0784f83c357260cec0.png) donde
donde  y
y  . [4] Esta función se llama función de distorsión o función de transformación de Wang.
. [4] Esta función se llama función de distorsión o función de transformación de Wang.
El función dual de la distorsión es  .[5][6] Dado un espacio probabilístico
.[5][6] Dado un espacio probabilístico 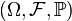 , entonces para cualquier variable aleatoria
, entonces para cualquier variable aleatoria  y cualquier función de distorsión
y cualquier función de distorsión  podemos definir un nuevo medida de la probabilidad
podemos definir un nuevo medida de la probabilidad  tal que para cualquier
tal que para cualquier 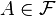 se deduce que
se deduce que  [5]
[5]
- Principio actuarial premium
Para cualquier función cóncava creciente de transformación Wang, podríamos definir un principio prima correspondiente:[4] 
- Medida de riesgo coherente
Una medida coherente de riesgo podría ser definida por una transformación de Wang de la función de distribución decumulative  y si sólo si
y si sólo si  es cóncavo.[4]
es cóncavo.[4]
Ejemplos de medida de riesgo
Valor en riesgo
Es bien sabido valor en riesgo No es, en general, una medida de riesgo coherente ya que no respeta la propiedad sub-aditividad. Una consecuencia inmediata es valor en riesgo podría desalentar la diversificación.[1] Valor en riesgo Sin embargo, es coherente, bajo el supuesto de elíptico distribuidos las pérdidas (ej.: distribuye normalmente) cuando el valor de la cartera es una función lineal de los precios de los activos. Sin embargo, en este caso el valor en riesgo llega a ser equivalente a un enfoque de media-varianza donde el riesgo de una cartera se mide por la variación de la rentabilidad de la cartera.
Es la función de transformación Wang (función de distorsión) para el valor en riesgo  . La no-concavidad de
. La no-concavidad de  demuestra la coherencia no de esta medida de riesgo.
demuestra la coherencia no de esta medida de riesgo.
- Ilustración
Como un ejemplo simple para demostrar la no-coherencia de value-at-risk considere mirando el VaR de un portafolio de confianza del 95% durante el próximo año de dos por defecto-able denominados bonos de cupón cero que maduran dentro de 1 años en nuestra moneda numeraria.
Supongamos la siguiente:
- El rendimiento actual de los dos bonos es 0%
- Los dos bonos son de diferentes emisores
- Cada bonos tiene un 4% probabilidad de incumplimiento durante el próximo año
- El caso de incumplimiento de cualquier vínculo es independiente del otro
- En caso de incumplimiento los bonos tienen una tasa de recuperación del 30%
Bajo estas condiciones el 95% VaR para la celebración de cualquiera de los bonos es 0 puesto que la probabilidad de impago es inferior al 5%. Sin embargo si llevamos a cabo un portafolio que consistió en un 50% de cada bono por valor de entonces el 95% VaR es 35% desde la probabilidad de que al menos uno de los bonos impagos es 7.84% que supera el 5%. Esto viola la propiedad sub-aditividad mostrando que el VaR no es una medida de riesgo coherente.
Promedio del valor en riesgo
El promedio del valor en riesgo (a veces llamado déficit esperado o valor en riesgo condicional) es una medida coherente de riesgo, aunque se deriva de valor en riesgo que no es.
Entrópico valor en riesgo
El entrópico valor en riesgo es una medida de riesgo coherente.[7]
Cola de valor en riesgo
El cola de valor en riesgo (o expectativa condicional de la cola) es una medida de riesgo coherente sólo cuando la distribución subyacente es continua.
La función de transformación Wang (función de distorsión) para el cola de valor en riesgo es  . La concavidad de
. La concavidad de  Comprueba la coherencia de esta medida del riesgo en el caso de distribución continua.
Comprueba la coherencia de esta medida del riesgo en el caso de distribución continua.
Medida proporcional del riesgo peligro (PH)
La medida del riesgo de PH (o medida del riesgo riesgo proporcional) transforma las tarifas hasard 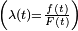 utilizando un coeficiente
utilizando un coeficiente  .
.
La función de transformación de Wang (función de distorsión) para la medida del riesgo PH es  . La concavidad de
. La concavidad de  If
If  Comprueba la coherencia de esta medida de riesgo.
Comprueba la coherencia de esta medida de riesgo.

medidas de riesgo g-entrópico
medidas de riesgo g-entrópico son una clase de medidas de riesgo información teórica coherente que involucran algunos casos importantes como el CVaR y EVaR.[7]
La medida del riesgo Wang
El medida del riesgo es de Wang para definir la siguiente función de transformación de Wang (función de distorsión) ![g_{\alpha}(x)=\Phi\left[ \Phi^{-1}(x)-\Phi^{-1}(\alpha)\right]](http://upload.wikimedia.org/math/3/c/1/3c139fdc52e138d4055f659aeb066c68.png) . La coherencia de esta medida de riesgo es una consecuencia de la concavidad de
. La coherencia de esta medida de riesgo es una consecuencia de la concavidad de  .
.
Medida del riesgo entrópica
El medida del riesgo entrópica es una medida de riesgo convexo que no es coherente. Se relaciona con la utilidad exponencial.
Precio Superhedging
El precio superhedging es una medida de riesgo coherente.
Conjunto de valores
En una situación con  -valorado carteras que riesgo puede medirse en
-valorado carteras que riesgo puede medirse en 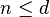 de los activos, entonces un conjunto de carpetas es la forma correcta de representar riesgo. Medidas de riesgo conjunto de valores son útiles para los mercados con costos de transacción.[8]
de los activos, entonces un conjunto de carpetas es la forma correcta de representar riesgo. Medidas de riesgo conjunto de valores son útiles para los mercados con costos de transacción.[8]
Propiedades
Una medida de riesgo coherente valores de conjunto es una función  , donde
, donde  y
y 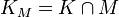 donde
donde  es una constante cono de solvencia y
es una constante cono de solvencia y  es el conjunto de carpetas de la
es el conjunto de carpetas de la  bienes de referencia.
bienes de referencia.  debe tener las siguientes propiedades:[9]
debe tener las siguientes propiedades:[9]
- Normalizado
-
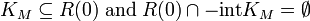
- Traslativo de M
-

- Monotono
-

- Sublinear
Medida del valor conjunto convexo riesgo
Si en lugar de la propiedad sublinear,R es convexo, entonces R es una medida de valor conjunto convexo riesgo.
Representación doble
A bajar semi-continuo medida del riesgo convexo  puede ser representado como
puede ser representado como
tal que  es un función de la pena y
es un función de la pena y 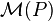 es el conjunto de medidas de probabilidad absolutamente continua con respecto a P (el "mundo real" medida de la probabilidad), es decir,
es el conjunto de medidas de probabilidad absolutamente continua con respecto a P (el "mundo real" medida de la probabilidad), es decir,  .
.
A bajar semi-continuo medida del riesgo es coherente si y sólo si se puede representar como
tal que  .[10]
.[10]
Véase también
- Métricas de riesgo -el concepto abstracto que cuantifica una medida del riesgo
- RiskMetrics -un modelo de gestión de riesgos
- Medida del riesgo espectral -un subconjunto de medidas de riesgo coherentes
- Medida del riesgo de distorsión
- Valor en riesgo condicional
- Entrópico valor en riesgo
- Riesgo financiero
Referencias
- ^ a b Artzner, P.; Delbaen, f el.; Eber, J. M.; Heath, D. (1999). "Medidas coherentes de riesgo". Matemática financiera 9 (3): 203. Doi:10.1111/1467-9965.00068.
- ^ Wilmott, P. (2006). "Finanzas Cuantitativas" 1 (2 ed.). Wiley. p. 342.
- ^ Föllmer, H.; Schied, A. (2002). "Convexas medidas de riesgo y las restricciones de comercio". Finanzas y Stochastics 6 (4): 429 – 447. Doi:10.1007/s007800200072.
- ^ a b c Wang, Shuan (1996). "Cálculo de la prima mediante la transformación de la capa superior densidad". Boletín de ASTIN 26 (1): 71-92. Doi:10.2143/AST.26.1.563234.
- ^ a b Balbás, A.; Garrido, J.; Mayoral, S. (2008). "Propiedades de las medidas de riesgo de distorsión". Metodología y cálculo de probabilidad aplicada 11 (3): 385. Doi:10.1007/s11009-008-9089-z.
- ^ Julia L. Wirch; Mary R. Hardy. "Las medidas de riesgo de distorsión: coherencia y dominio estocástico" (pdf). 10 de marzo de 2012.
- ^ a b Ahmadi-Javid, Amir (2012). "Value-at-risk entrópico: una nueva medida de riesgo coherente". Diario de optimización teoría y aplicaciones 155 (3): 1105-1123. Doi:10.1007/s10957-011-9968-2.
- ^ Jouini, Elyes; Meddeb, Moncef; Touzi, Nizar (2004). "Medidas de riesgo coherentes vector – valorado". Finanzas y Stochastics 8 (4): 531-552. Doi:10.1007/s00780-004-0127-6.
- ^ Hamel, A. H.; Heyde, f el. (2010). "Dualidad por valor conjunto de medidas de riesgo" (pdf). SIAM Journal on matemáticas financieras 1 (1): 66 – 95. Doi:10.1137/080743494. 17 de agosto de 2012.
- ^ Föllmer, Hans; Schied, Alexander (2004). Finanzas estocástico: una introducción en tiempo discreto (2 ed.). Walter de Gruyter. ISBN978-3-11-018346-7.
Enlaces externos
- Una lista de documentos importantes en medidas de riesgo coherentes y convexo

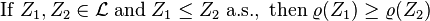

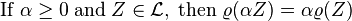

![If \ Z_1,Z_2 \in \mathcal{L}\text{ and }\lambda \in [0,1] \text{ then }\varrho(\lambda Z_1 + (1-\lambda) Z_2) \leq \lambda \varrho(Z_1) + (1-\lambda) \varrho(Z_2)](http://upload.wikimedia.org/math/9/7/7/9776e40f411fa860810a0706d7b326f3.png)
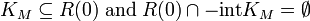


![\varrho(X) = \sup_{Q \in \mathcal{M}(P)} \{E^Q[-X] - \alpha(Q)\}](http://upload.wikimedia.org/math/9/b/d/9bdf71fcf7fd52bdd0663b54101da80d.png)
![\varrho(X) = \sup_{Q \in \mathcal{Q}} E^Q[-X]](http://upload.wikimedia.org/math/7/e/3/7e3a2934a9e7ce3b4153c105e1a79787.png)