Punto establece registro

En visión por computador y reconocimiento de patrones, punto de registro establecido, también conocido como punto de coincidencia, es el proceso de encontrar un espacial transformación alinea dos conjuntos de punto. El propósito de encontrar una transformación incluye combinar múltiples conjuntos de datos en un modelo consistente en todo el mundo y asignar una nueva medición a un conjunto de datos conocido para identificar las características o estimar su pose. Un sistema del punto puede ser datos crudos de Digitalización 3D o una matriz de Telémetros. Para su uso en procesamiento y basado en funciones de la imagen registro de la imagen, un sistema del punto puede ser un conjunto de características obtenidas por extracción de la característica de una imagen, por ejemplo detección de esquina. Registro conjunto de punto se utiliza en reconocimiento óptico de caracteres[1][2] y la alineación de los datos de imágenes por resonancia magnética con tomografía asistida por computadora exploraciones.[3][4]
Contenido
- 1 Descripción del problema
- 1.1 Registro rígido
- 1.2 Registro no rígidos
- 2 Punto establece algoritmos de registro
- 2.1 Punto más cercano iterativo
- 2.2 Punto robusto que empareja
- 2.2.1 Placa delgada tira punto robusto que empareja
- 2.3 Correlación del núcleo
- 2.3.1 Modelo gaussiano mezcla
- 2.4 Punto coherente deriva
- 3 Enlaces externos
- 4 Referencias
Descripción del problema


El problema puede ser resumido como sigue:[5] Dejar 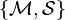 ser dos sistemas del punto tamaño finito in un verdadero espacio finito-dimensional del vector
ser dos sistemas del punto tamaño finito in un verdadero espacio finito-dimensional del vector  , que contienen
, que contienen  y
y  puntos respectivamente. El problema es encontrar una transformación que se aplicará a la configuración de puntos móviles de "modelo"
puntos respectivamente. El problema es encontrar una transformación que se aplicará a la configuración de puntos móviles de "modelo" 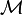 tal que la diferencia entre
tal que la diferencia entre 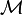 y la estática "escena"
y la estática "escena"  se minimiza. En otras palabras, una asignación de
se minimiza. En otras palabras, una asignación de  Para
Para  es deseado que rinde la mejor alineación entre la transformada "modelo" y la "escena". La asignación puede consistir en una transformación rígida o deformable. El modelo de transformación puede ser escrito como
es deseado que rinde la mejor alineación entre la transformada "modelo" y la "escena". La asignación puede consistir en una transformación rígida o deformable. El modelo de transformación puede ser escrito como  registrado el transformado, modelo punto conjunto es:
registrado el transformado, modelo punto conjunto es:
-

()
Es útil definir un parámetro de la optimización  :
:
-

()
Así está claro que el algoritmo de optimización ajusta  . Dependiendo del problema y el número de dimensiones, puede haber más dichos parámetros. La salida de un algoritmo de registro conjunto punto por lo tanto es el parámetro de transformación
. Dependiendo del problema y el número de dimensiones, puede haber más dichos parámetros. La salida de un algoritmo de registro conjunto punto por lo tanto es el parámetro de transformación  del modelo
del modelo  Para
Para 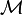 está perfectamente alineado con
está perfectamente alineado con  .
.
En la convergencia, que es deseable para la distancia entre los dos conjuntos de punto para llegar a un mínimo global. Es difícil sin agotar todas las transformaciones posibles, así que basta un mínimo local. Establece la función de la distancia entre un punto modelo transformado  y el sistema de punto de la escena
y el sistema de punto de la escena  se da por cierta función
se da por cierta función  . Es un enfoque sencillo para tomar la Plaza de la Distancia euclidiana para cada par de puntos:
. Es un enfoque sencillo para tomar la Plaza de la Distancia euclidiana para cada par de puntos:
-
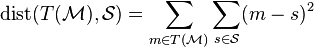
()
Minimizar tal función en registro rígido es equivalente a resolver una mínimos cuadrados problema. Sin embargo, esta función es sensible a los datos aislados y en consecuencia algoritmos basados en esta función tienden a ser menos robusto contra datos ruidosos. Una formulación más robusta de la función de costo utiliza algunos función robusta  :
:
-
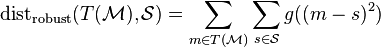
()
Una formulación tan es conocida como un M-estimador. La función robusta  se elige tal que la configuración local de la configuración de puntos es insensible a puntos distantes, por lo tanto, por lo que es robusto contra ruido y afloramientos.[6]
se elige tal que la configuración local de la configuración de puntos es insensible a puntos distantes, por lo tanto, por lo que es robusto contra ruido y afloramientos.[6]
Registro rígido
Dados dos conjuntos de punto, registro rígido produce un transformación rígida que asigna un punto a otro. Una transformación rígida se define como una transformación que no cambia la distancia entre dos puntos cualesquiera. Típicamente consiste en una transformación traducción y rotación.[2] En casos raros, también puede reflejarse la configuración de puntos.
Registro no rígidos
Dados dos conjuntos de punto, registro deformable produce una transformación no rígidos que se asigna un sistema del punto a la otra. Incluyen transformaciones non-rígido transformaciones afines tales como escalamiento y cizalla mapeo. Sin embargo, en el contexto del punto determinado registro, registro deformable implica típicamente transformación no lineal. Si el eigenmodes de variación del punto de juego son conocidas, la transformación no lineal puede ser parametrizados por los valores propios.[7] Una transformación no lineal también puede ser parametrizados como un tira fina de la placa.[1][7]
Punto establece algoritmos de registro
Algunos enfoques al punto de registro conjunto utilizan algoritmos que resuelven la más general gráfico que empareja problema.[5] Sin embargo, la complejidad computacional de tales métodos tienden a ser altos y están limitados a los registros rígidos. En las siguientes secciones se describen algoritmos específicos para el problema de registro conjunto de punto.
Punto más cercano iterativo
El punto más cercano iterativo Algoritmo (ICP) fue introducida por Besl y McKay.[8] El algoritmo realiza registro rígido en forma iterativa por suponiendo que cada punto en 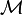 se corresponde con el punto más cercano a él en
se corresponde con el punto más cercano a él en  y luego encontrar el mínimos cuadrados transformación rígida. Como tal, funciona mejor si plantean la inicial de
y luego encontrar el mínimos cuadrados transformación rígida. Como tal, funciona mejor si plantean la inicial de 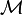 está lo suficientemente cerca
está lo suficientemente cerca  . En pseudocódigo, se implementa el algoritmo básico como sigue:
. En pseudocódigo, se implementa el algoritmo básico como sigue:
Algoritmo de ICP
:=
mientras que no está registrado:
:=
para
::
: = punto más cercano en
Para

:=
+

:= mínimos cuadrados
retorno

Aquí, la función least_squares realiza mínimos cuadrados regresión para reducir al mínimo la distancia en cada uno de los  pares, es decir, minimizando la función distancia en la ecuación ()3).
pares, es decir, minimizando la función distancia en la ecuación ()3).
Porque el función de coste del registro depende de encontrar el punto más cercano en  a cada punto de
a cada punto de 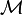 , puede cambiar mientras se ejecuta el algoritmo. Por lo tanto, es difícil de probar que el ICP se reunirán en realidad exactamente a los óptimos locales.[6] De hecho, empíricamente, ICP y EM-ICP no convergen al mínimo local de la función de costo.[6] Sin embargo, porque el ICP es intuitivo de entender y fácil de implementar, sigue siendo el algoritmo de registro conjunto punto más comúnmente utilizado.[6] Se han propuesto muchas variantes del ICP, que afecta a todas las fases del algoritmo de la selección y coincidencia de puntos de la estrategia de minimización.[7][9] Por ejemplo, la maximización de la expectativa algoritmo se aplica el algoritmo ICP para formar el método EM-ICP y la Algoritmo de Levenberg-Marquardt se aplica el algoritmo ICP para formar el método de la LM-ICP.[2]
, puede cambiar mientras se ejecuta el algoritmo. Por lo tanto, es difícil de probar que el ICP se reunirán en realidad exactamente a los óptimos locales.[6] De hecho, empíricamente, ICP y EM-ICP no convergen al mínimo local de la función de costo.[6] Sin embargo, porque el ICP es intuitivo de entender y fácil de implementar, sigue siendo el algoritmo de registro conjunto punto más comúnmente utilizado.[6] Se han propuesto muchas variantes del ICP, que afecta a todas las fases del algoritmo de la selección y coincidencia de puntos de la estrategia de minimización.[7][9] Por ejemplo, la maximización de la expectativa algoritmo se aplica el algoritmo ICP para formar el método EM-ICP y la Algoritmo de Levenberg-Marquardt se aplica el algoritmo ICP para formar el método de la LM-ICP.[2]
Punto robusto que empareja
Sólido punto de coincidencia (RPM) fue introducido por oro et al.[10] El método realiza registro usando recocido determinista y suave permite la asignación de las correspondencias entre conjuntos de punto. Mientras que en el ICP la correspondencia generada por la heurística más cercano vecino binaria, RPM utiliza un suave correspondencia donde la correspondencia entre dos puntos cualquiera puede ser en cualquier lugar de 0 a 1, aunque en última instancia, converge a 0 o 1. Las correspondencias encontramos RPM es siempre uno a uno, que no siempre es el caso de ICP.[1] Dejar  ser el
ser el  punto de TH en
punto de TH en 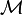 y
y  ser el
ser el  punto de TH en
punto de TH en  . El coincidir con matriz
. El coincidir con matriz 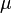 se define como tal:
se define como tal:
-

()
El problema entonces se define como: dados dos conjuntos de punto 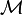 y
y  encontrar el Transformación afín
encontrar el Transformación afín  y la matriz de fósforo
y la matriz de fósforo 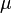 que mejor se les relaciona.[10] Conociendo la transformación óptima hace que sea fácil determinar la matriz de fósforo y viceversa. Sin embargo, el algoritmo RPM determina ambos simultáneamente. La transformación se puede descomponer en un vector de traslación y una matriz de transformación:
que mejor se les relaciona.[10] Conociendo la transformación óptima hace que sea fácil determinar la matriz de fósforo y viceversa. Sin embargo, el algoritmo RPM determina ambos simultáneamente. La transformación se puede descomponer en un vector de traslación y una matriz de transformación:
La matriz  en 2D se compone de cuatro parámetros separados
en 2D se compone de cuatro parámetros separados  , que son de escala, rotación y la vertical y horizontal del esquileo componentes respectivamente. La función de costo es entonces:
, que son de escala, rotación y la vertical y horizontal del esquileo componentes respectivamente. La función de costo es entonces:
-

()
sujeto a  ,
,  ,
,  . El
. El  término predispone el objetivo hacia más fuerte correlación disminuyendo el costo si la matriz partido tiene más en él. La función
término predispone el objetivo hacia más fuerte correlación disminuyendo el costo si la matriz partido tiene más en él. La función  sirve para regularizar la transformación afín penalizar el valuse grande de la escala y distorsionar los componentes:
sirve para regularizar la transformación afín penalizar el valuse grande de la escala y distorsionar los componentes:
para un parámetro de regularización  .
.
El método RPM optimiza la función de costo utilizando la Softassign algoritmo. Aquí se derivará el caso 1D. Dado un conjunto de variables 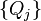 donde
donde  . Una variable
. Una variable  se asocia a cada uno
se asocia a cada uno  tal que
tal que  . El objetivo es encontrar
. El objetivo es encontrar 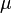 maximiza
maximiza  . Esto puede ser formulado como un problema continuo mediante la introducción de un parámetro de control
. Esto puede ser formulado como un problema continuo mediante la introducción de un parámetro de control  . En recocido determinista método, el parámetro de control
. En recocido determinista método, el parámetro de control  se incrementa lentamente mientras el algoritmo corre. Dejar
se incrementa lentamente mientras el algoritmo corre. Dejar 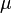 ser:
ser:
-

()
Esto se conoce como el función softmax. Como  aumenta, se aproxima a un valor binario según lo deseado en la ecuación)rpm.1). El problema puede ser generalizado al caso 2D, donde en lugar de maximizar
aumenta, se aproxima a un valor binario según lo deseado en la ecuación)rpm.1). El problema puede ser generalizado al caso 2D, donde en lugar de maximizar  , se maximiza la siguiente:
, se maximiza la siguiente:
-
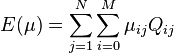
()
donde
Esto es sencillo, excepto que ahora las restricciones en  son matriz doblemente estocástica restricciones:
son matriz doblemente estocástica restricciones:  y
y  . Como tal el denominador de la ecuación)rpm.3) no puede ser expresado para el caso 2D simplemente. Para satisfacer las restricciones, es posible usar un resultado debido a Sinkhorn,[10] lo que significa que una matriz doblemente estocástica es obtenida de cualquier matriz cuadrada con todas las entradas positivas por el proceso iterativo de alternancia normalizar de fila y columna. Así está escrito como tal el algoritmo:[10]
. Como tal el denominador de la ecuación)rpm.3) no puede ser expresado para el caso 2D simplemente. Para satisfacer las restricciones, es posible usar un resultado debido a Sinkhorn,[10] lo que significa que una matriz doblemente estocástica es obtenida de cualquier matriz cuadrada con todas las entradas positivas por el proceso iterativo de alternancia normalizar de fila y columna. Así está escrito como tal el algoritmo:[10]
Algoritmo RPM2D
: = 0
: = 0
:=

:=
al mismo tiempo
:: mientras que
No ha convergido: actualización de parámetros de correspondencia por softassign
:=

:=
aplicar el método de Sinkhorn al mismo tiempo
No ha convergido: actualización
por la normalización a través de todas las filas:
:=
actualización
por la normalización a través de todas las columnas:
:=
actualización plantean parámetros por coordenadas pendiente actualización
usando solución analítica update
usando solución analítica update
usando Método de Newton
:=

:=
retorno
y
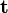
donde el recocido determinista control de parámetro  se establece inicialmente en
se establece inicialmente en  y los aumentos por factor
y los aumentos por factor 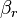 hasta que alcanza el valor máximo
hasta que alcanza el valor máximo  . Las adiciones en la suma de medidas de normalización de
. Las adiciones en la suma de medidas de normalización de  y
y 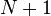 en lugar de sólo
en lugar de sólo  y
y  porque las restricciones
porque las restricciones  son las desigualdades. Como tal el
son las desigualdades. Como tal el  TH y
TH y 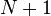 son elementos de TH variables de holgura.
son elementos de TH variables de holgura.
El algoritmo también puede ampliarse para conjuntos de punto en 3D o mayores dimensiones. Las restricciones sobre la matriz de correspondencia 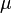 son las mismas en el caso como en el caso 2D 3D. Por lo tanto, la estructura del algoritmo permanece sin cambios, con la diferencia principal es cómo se resuelven las matrices de rotación y traslación.[10]
son las mismas en el caso como en el caso 2D 3D. Por lo tanto, la estructura del algoritmo permanece sin cambios, con la diferencia principal es cómo se resuelven las matrices de rotación y traslación.[10]
Placa delgada tira punto robusto que empareja

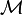 el magenta punto conjunto
el magenta punto conjunto
 corrompidas con afloramientos ruidosos. El tamaño de los círculos azules está inversamente relacionado con el parámetro de control
corrompidas con afloramientos ruidosos. El tamaño de los círculos azules está inversamente relacionado con el parámetro de control
 . Las líneas amarillas indican correspondencia.
. Las líneas amarillas indican correspondencia.
El algoritmo que empareja (TPS-RPM) de placa delgada spline robusto punto por Chui y Rangarajan aumenta el método RPM para realizar registro deformable por oponeros la transformación como un tira fina de la placa.[1] Sin embargo, porque la placa delgada tira parametrización sólo existe en tres dimensiones, el método no puede ampliarse a los problemas que implica cuatro o más dimensiones.
Correlación del núcleo
El enfoque de correlación (KC) del núcleo del punto de registro conjunto fue introducido por Tsin y Kanade.[6] Comparado con el ICP, el algoritmo KC es más robusto contra datos ruidosos. A diferencia de ICP, donde, para cada punto de modelo, se considera solamente el punto más cercano de la escena, aquí cada escena punto afecta a todos los puntos del modelo.[6] Como tal es un multiplicar-ligado algoritmo de registro. Para algunos función del núcleo  , la correlación del núcleo
, la correlación del núcleo  de dos puntos
de dos puntos  se define así:[6]
se define así:[6]
-

()
El función del núcleo  elegido para punto de registro del sistema es típicamente simétrica y no negativo kernel, similar a las utilizadas en la Ventana de Parzen estimación de densidad. El Núcleo gaussiano típicamente utilizado por su sencillez, aunque otros como el Núcleo Epanechnikov y el núcleo tricube puede ser substituido.[6] Establece la correlación del núcleo de un punto entero
elegido para punto de registro del sistema es típicamente simétrica y no negativo kernel, similar a las utilizadas en la Ventana de Parzen estimación de densidad. El Núcleo gaussiano típicamente utilizado por su sencillez, aunque otros como el Núcleo Epanechnikov y el núcleo tricube puede ser substituido.[6] Establece la correlación del núcleo de un punto entero 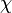 se define como la suma de las correlaciones del núcleo de cada punto en el conjunto de todos los otros puntos en el conjunto:[6]
se define como la suma de las correlaciones del núcleo de cada punto en el conjunto de todos los otros puntos en el conjunto:[6]
-

()
El KC de un sistema del punto es proporcional, dentro de un factor constante, el logaritmo de entropía (teoría de la información). Observar que el KC es una medida de un "compactación" de la configuración de puntos — trivial, si todos los puntos en la configuración de puntos estaban en el mismo lugar, el KC evaluaría a cero. El función de coste del punto de establece registro algoritmo para algunos parámetros de transformación  se define así:
se define así:
-
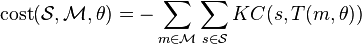
()
Algunas producciones de manipulación algebraica:
-

()
La expresión se simplifica mediante la observación de  es independiente de
es independiente de  . Además, suponiendo que registro rígido, KC (T (\mathcal {M}, \theta)) es invariante cuando
. Además, suponiendo que registro rígido, KC (T (\mathcal {M}, \theta)) es invariante cuando  ha cambiado porque la distancia euclidiana entre cada par de puntos sigue siendo el mismo bajo transformación rígida. Así que la ecuación anterior puede ser reescrita como:
ha cambiado porque la distancia euclidiana entre cada par de puntos sigue siendo el mismo bajo transformación rígida. Así que la ecuación anterior puede ser reescrita como:
-
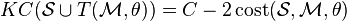
()
El estimaciones de la densidad del núcleo se definen como:
La función de costo entonces puede ser demostrada que la correlación de las estimaciones de la densidad del dos núcleo:
-

()
Habiendo establecido la función de coste, simplemente utiliza el algoritmo descenso de gradiente para encontrar la transformación óptima. Es computacionalmente caro calcular la función de costo desde cero en cada iteración, para una versión discreta del coste la función (ecuaciónKC.6) se utiliza. Las estimaciones de la densidad del núcleo  puede ser evaluado en puntos de la cuadrícula y almacenados en un tabla de consulta. A diferencia de la ICP y métodos relacionados, no es necesario financiar al vecino más cercano, que permite que el algoritmo de KC para ser comparativamente simple en ejecución.
puede ser evaluado en puntos de la cuadrícula y almacenados en un tabla de consulta. A diferencia de la ICP y métodos relacionados, no es necesario financiar al vecino más cercano, que permite que el algoritmo de KC para ser comparativamente simple en ejecución.
Comparado con ICP y EM-ICP para sistemas del ruidoso punto 2D y 3D, el algoritmo KC es menos sensible al ruido y resultados en la correcta inscripción más a menudo.[6]
Modelo gaussiano mezcla
Las estimaciones de la densidad del núcleo son sumas de Gaussianas y por lo tanto pueden ser representadas como Modelos de mezcla gaussiano (GMM).[11] Jian y Vemuri utilizan la versión GMM del algoritmo de registro KC realizar registro deformable parametrizadas por ranuras de la placa delgada.
Punto coherente deriva

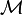 punto rojo conjunto
punto rojo conjunto
 usando el algoritmo deriva punto coherente. Ambos conjuntos de punto han sido corrompidas con puntos quitados y aislados espurio al azar.
usando el algoritmo deriva punto coherente. Ambos conjuntos de punto han sido corrompidas con puntos quitados y aislados espurio al azar.

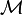 punto rojo conjunto
punto rojo conjunto
 usando el algoritmo deriva punto coherente.
usando el algoritmo deriva punto coherente.

 punto rojo conjunto
punto rojo conjunto
 usando el algoritmo deriva punto coherente. Ambos conjuntos de punto han sido corrompidas con puntos quitados y aislados espurio al azar.
usando el algoritmo deriva punto coherente. Ambos conjuntos de punto han sido corrompidas con puntos quitados y aislados espurio al azar.
Punto coherente deriva (CPD) fue introducida por Myronenko y la canción.[7][12] El algoritmo toma un enfoque probabilístico a alinear sistemas del punto, similar al método GMM KC. A diferencia de enfoques anteriores al registro deformable que asumen un tira fina de la placa modelo de transformación, CPD es agnóstica en relación con el modelo de transformación utilizado. El sistema del punto 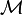 representa el Modelo gaussiano mezcla Centroides (GMM). Cuando los dos conjuntos de punto óptimo estén alineados, la correspondencia es el máximo del MGM probabilidad posterior para un punto de datos determinado. Para preservar la estructura topológica de los conjuntos de punto, los centroides GMM son forzados a moverse coherente como grupo. El maximización de la expectativa algoritmo se utiliza para optimizar la función de costo.[7]
representa el Modelo gaussiano mezcla Centroides (GMM). Cuando los dos conjuntos de punto óptimo estén alineados, la correspondencia es el máximo del MGM probabilidad posterior para un punto de datos determinado. Para preservar la estructura topológica de los conjuntos de punto, los centroides GMM son forzados a moverse coherente como grupo. El maximización de la expectativa algoritmo se utiliza para optimizar la función de costo.[7]
Hágase  puntos en
puntos en 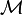 y
y  puntos en
puntos en  . El GMM función de densidad de probabilidad para un punto
. El GMM función de densidad de probabilidad para un punto  es:
es:
-

()
donde, en  dimensiones,
dimensiones,  es el Distribución Gausiana centrado en el punto
es el Distribución Gausiana centrado en el punto  .
.
Las probabilidades de pertenencia  es igual para todos los componentes GMM. El peso de la distribución uniforme se denota como
es igual para todos los componentes GMM. El peso de la distribución uniforme se denota como ![w\in[0,1]](http://upload.wikimedia.org/math/c/1/b/c1b1b7698d2deeeb01c3d1e608be196d.png) . El modelo de mezcla es entonces:
. El modelo de mezcla es entonces:
-
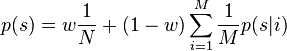
()
Los centroides GMM son re-parametrizadas por un conjunto de parámetros  Estimado maximizando la probabilidad. Esto es equivalente a minimizar el negativo función log-verosimilitud:
Estimado maximizando la probabilidad. Esto es equivalente a minimizar el negativo función log-verosimilitud:
-

()
donde se supone que los datos sean independientes e idénticamente distribuidas. La probabilidad de correspondencia entre dos puntos  y
y  se define como el probabilidad posterior del MGM centroide dado el punto de datos:
se define como el probabilidad posterior del MGM centroide dado el punto de datos:
El maximización de la expectativa Algoritmo (EM) se usa para encontrar  y
y  . El algoritmo EM consta de dos pasos. Primero, en el paso E o estimación paso, adivina los valores de los parámetros (valores de parámetro "viejo") y luego usa Teorema de Bayes para calcular las distribuciones de probabilidad posteriores
. El algoritmo EM consta de dos pasos. Primero, en el paso E o estimación paso, adivina los valores de los parámetros (valores de parámetro "viejo") y luego usa Teorema de Bayes para calcular las distribuciones de probabilidad posteriores  de los componentes de la mezcla. Segundo, en el paso M o maximización paso, luego se encuentran los valores del parámetro "nuevo" reduciendo la expectativa de la función log-verosimilitud negativa completa, es decir, la función de coste:
de los componentes de la mezcla. Segundo, en el paso M o maximización paso, luego se encuentran los valores del parámetro "nuevo" reduciendo la expectativa de la función log-verosimilitud negativa completa, es decir, la función de coste:
-

()
Ignorando las constantes independientes de  y
y  () EcuaciónCPD.4) puede ser expresado así:
() EcuaciónCPD.4) puede ser expresado así:
-
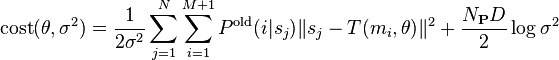
()
donde
con 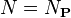 Sólo si
Sólo si 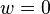 . Las probabilidades de GMM componentes calculados utilizando los valores de parámetro anterior posteriores
. Las probabilidades de GMM componentes calculados utilizando los valores de parámetro anterior posteriores  es:
es:
-
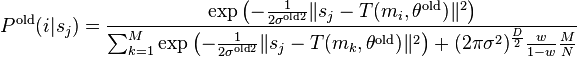
()
Minimizando la función de costo en la ecuación)CPD.5) necesariamente disminuye la función log-verosimilitud negativa  en la ecuación)CPD.3) a menos que ya está en un mínimo local.[7] Por lo tanto, el algoritmo puede ser expresado mediante la siguiente pseudocódigo, donde se pone el punto
en la ecuación)CPD.3) a menos que ya está en un mínimo local.[7] Por lo tanto, el algoritmo puede ser expresado mediante la siguiente pseudocódigo, donde se pone el punto 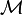 y
y  se representan como
se representan como 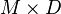 y
y  matrices
matrices  y
y  respectivamente:[7]
respectivamente:[7]
Algoritmo de CPD
:=
inicializar
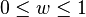
:=
mientras que no está registrado: E-paso, cálculo
para
y
::
:=
M-paso, resolver la transformación óptima
:= resolver
retorno

donde el vector  es un vector columna de unos. El
es un vector columna de unos. El resolver función diferencia por el tipo de registro realizado. Por ejemplo, en el registro rígido, la salida es una escala  , una matriz de rotación
, una matriz de rotación 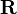 y un vector de traslación
y un vector de traslación 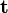 . El parámetro
. El parámetro  puede escribirse como una tupla de éstos:
puede escribirse como una tupla de éstos:
que se inicializa en uno, el matriz identidady un vector columna de ceros:
Es el conjunto de puntos alineados:
El solve_rigid función de registro rígido puede escribirse entonces como sigue, con derivación de la álgebra explicada en papel de Myronenko 2010.[7]
solve_rigid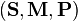
:=
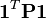
:=
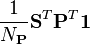
:=

:=
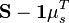
:=
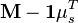
:=
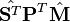
:= SVD
el descomposición de valor singular de
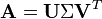
:=
//
es el matriz diagonal formado a partir de vectores

:=
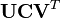
:=
//
es el rastro de una matriz
:=

:=
retorno
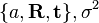
Para el registro afín, donde el objetivo es encontrar un Transformación afín en lugar de uno rígido, el resultado es una matriz de transformación afín  y una traducción
y una traducción 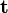 tal que el conjunto de puntos alineados:
tal que el conjunto de puntos alineados:
El solve_affine función de registro rígido puede escribirse entonces como sigue, con derivación de la álgebra explicada en papel de Myronenko 2010.[7]
solve_affine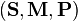
:=
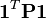
:=
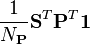
:=

:=
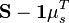
:=
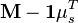
:=
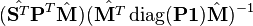
:=
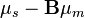
:=
retorno

También es posible utilizar CPD con registro deformable usando una parametrización derivado usando cálculo de la variación.[7]
Las sumas de las distribuciones gaussianas pueden ser computadas en tiempo lineal usando el transformación rápida de Gauss (FGT).[7] En consecuencia, la complejidad de tiempo de CPD es 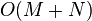 , que es asintóticamente mucho más rápido que
, que es asintóticamente mucho más rápido que  métodos.[7]
métodos.[7]
Enlaces externos
- Implementación de referencia de placa delgada tira punto robusto que empareja
- Implementación de referencia de punto de correlación del núcleo conjunto registro
- Implementación de referencia de punto coherente deriva
Referencias
- ^ a b c d Chui, Haili; Rangarajan, Anand (2003). "Un nuevo punto de coincidencia de algoritmo de registro no rígidos". Visión por computador y la interpretación de imágenes 89 (2): 114-141. Doi:10.1016/S1077-3142 (03) 00009-2.
- ^ a b c Fitzgibbon, Andrew W. (2003). "Registro robusto de 2D y 3D punto conjuntos". Imagen y visión informática 21 (13): 1145-1153. Doi:10.1016/j.imavis.2003.09.004.
- ^ Hill, Derek LG; Hawkes, J. D.; Crossman, J. E.; Gleeson, M. J.; Cox, T. C. S.; Bracey, E. E. C. M. L.; Strong, A. J.; Graves, P. (1991). "Registro de imágenes de Sr. y del CT para cirugía de base del cráneo usando características anatómicas puntuales". Revista británica de radiología 64 (767): 1030-1035. Doi:10.1259/0007-1285-64-767-1030.
- ^ Studholme, C.; Hill, L. D.; Hawkes, D. J. (1995). "Automated 3D registro del Sr. truncado e imágenes del CT de la cabeza". Actas de la sexta Conferencia de visión de máquina británico. PP. 27-36.
- ^ a b Jian, Bing; Vemuri, Baba C. (2011). "Registro robusto conjunto utilizando modelos de mezcla gaussiana". IEEE Transactions on análisis de patrones y de inteligencia de la máquina 33 (8): 1633 – 1645. Doi:10.1109/tpami.2010.223.
- ^ a b c d e f g h i j Tsin, Yanghai; Kanade, Takeo (2004). ' Una correlación-Based Approach to robusto conjunto registro'. Visión por computador ECCV (Springer Berlín Heidelberg): 558-569.
- ^ a b c d e f g h i j k l Myronenko, Andriy; Canción, Xubo (2010). "Punto establece registro: deriva del punto coherente". IEEE Transactions on análisis de patrones y de inteligencia de la máquina 32 (2): 2262-2275. Doi:10.1109/tpami.2010.46.
- ^ BESL, Neil; McKay (1992). "Un método para el registro de las formas tridimensionales". IEEE Transactions on análisis de patrones y de inteligencia de la máquina 14 (2): 239-256. Doi:10.1109/34.121791.
- ^ Rusinkiewicz, Szymon; Levoy, Marc (2001). "Variantes eficientes del algoritmo ICP". Actas de la tercera Conferencia Internacional sobre 3-d Digital de imagen y modelaje, 2001. IEEE. págs. 145-152. Doi:10.1109/IM.2001.924423.
- ^ a b c d e Oro, Steven; Rangarajan, Anand; Lu, Chien-Ping; Suguna, Pappu; Mjolsness, Eric (1998). "Nuevos algoritmos para 2d y 3d punto coincidente:: plantean estimación y correspondencia". Reconocimiento de patrones 38 (8): 1019 – 1031.
- ^ Jian, Bing; Vemuri, Baba C. (2005). "Un algoritmo robusto para punto de set registro usando mezcla de Gaussianas". Décimo IEEE International Conference on Computer Vision 2005 2. págs. 1246 – 1251.
- ^ Myronenko, Andriy; Canción, Xubo; Carriera-Perpinán, Miguel A. (2006). "Non-rígido punto establece registro: punto coherente deriva". Avances en sistemas de procesamiento de información Neural 19:: 1009-1016. 31 de mayo de 2014.

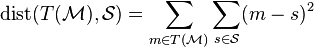
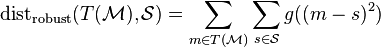

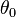 mientras que no está registrado:
mientras que no está registrado:  :=
:=  para
para  ::
:: 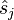 : = punto más cercano en
: = punto más cercano en  retorno
retorno 




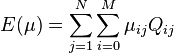
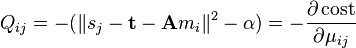
 : = 0
: = 0  :=
:=  al mismo tiempo
al mismo tiempo 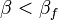 :: mientras que
:: mientras que  :=
:= 
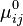 :=
:=  aplicar el método de Sinkhorn
al mismo tiempo
aplicar el método de Sinkhorn
al mismo tiempo  No ha convergido: actualización
No ha convergido: actualización  :=
:=  actualización
actualización  :=
:=  actualización plantean parámetros por coordenadas pendiente
actualización
actualización plantean parámetros por coordenadas pendiente
actualización  usando Método de Newton
usando Método de Newton

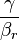 retorno
retorno  y
y 

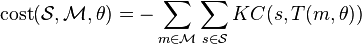

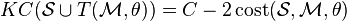




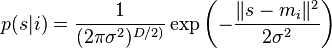
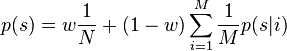

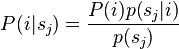

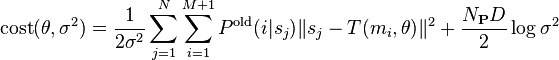

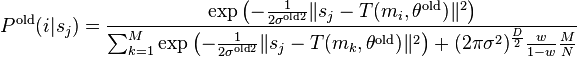
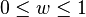
 mientras que no está registrado: E-paso, cálculo
mientras que no está registrado: E-paso, cálculo  para
para ![i\in [1,M]](http://upload.wikimedia.org/math/4/f/9/4f932e1d43adb9bb4a356b17bf5bc29e.png) y
y ![j\in [1,N]](http://upload.wikimedia.org/math/a/7/c/a7c4a8697d58042f90a745eee9a9be2b.png) ::
:: 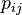 :=
:= 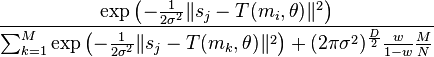 M-paso, resolver la transformación óptima
M-paso, resolver la transformación óptima
 := resolver
:= resolver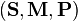 retorno
retorno 


 :=
:= 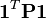
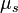 :=
:= 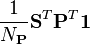
 :=
:= 
 :=
:= 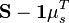
 :=
:= 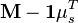
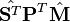
 := SVD
:= SVD el descomposición de valor singular de
el descomposición de valor singular de 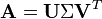
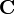 :=
:=  //
//  es el matriz diagonal formado a partir de vectores
es el matriz diagonal formado a partir de vectores 
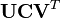
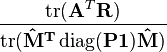 //
//  es el rastro de una matriz
es el rastro de una matriz

 retorno
retorno 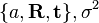

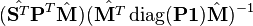
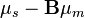
 retorno
retorno 