Economía de Robinson Crusoe

Para otras aplicaciones, vea Robinson Crusoe (desambiguación).

Parte de una serie en
Sistemas económicos
Por ideología Anarquista Capitalista Comunista Corporativista Dirigist Fascista Georgist Islámica El laissez-faire Socialista de mercado Mercantilista Neo-mercantilista Participativa Proteccionistas Socialista Capitalismo de estado Sindicalista
Por la coordinación Cerrado (autarquía) Descentralizado Digital Dual Regalo Informal Mercado Mixto Natural Abierto Planeado Robinson Crusoe Subsistencia Metro Archipiélago vertical Virtual
Según el modelo regional Anglosajón Chino Asia oriental Alemán Nórdico Renano Singapur Soviético
Sectores Propiedad común Privado Público Voluntario
Transición Colectivización Comunización Privatización Desmutualización Desregulación Expropiación Financiarización Liberalización Mercantilización Municipalización Mutualización Nacionalización Privatización Socialización
Coordinación Trueque Cibernética Democrática Mercado libre En la clase Planificación indicativa Mercado Material de equilibrio Planeado Peer-to-peer Precio Mercado regulado Autogestionado Compartido
Otros tipos Capitalismo corporativo Expedicionario Feudalismo Cazadores y recolectores Información Recientemente industrializados Palacio Plantation Post capitalista Post-industriales Post-escasez Basada en recursos Social de mercado Socialista de mercado Monopolio estatal capitalista Token Tradicional Transición Mundo
Portal de economía y negocios

A Economía de Robinson Crusoe se utiliza un simple marco para estudiar algunos temas fundamentales en la economía. Se supone que una economía con un consumidor, un productor y dos mercancías. El título"Robinson Crusoe"es una referencia a la novela del mismo nombre escrito por Daniel Defoe en 1719.

Como un experimento del pensamiento en economía, muchos economistas comercio internacional han encontrado esta versión simplificada e idealizada de la historia importante debido a su capacidad para simplificar la complejidad del mundo real. El supuesto implícito es que el estudio de la economía de un agente proporcionará útiles conocimientos sobre el funcionamiento de una economía mundial real con muchos agentes económicos. Este artículo se refiere al estudio de comportamiento del consumidor, comportamiento de productor y equilibrio como parte de la microeconomía. En otros campos de la economía, el marco de la economía de Robinson Crusoe se destina esencialmente la misma cosa. Por ejemplo, en finanzas públicas la economía de Robinson Crusoe se utiliza para estudiar los diferentes tipos de bienes públicos y ciertos aspectos de beneficios colectivos. Se utiliza en economía de crecimiento desarrollo de modelos de crecimiento para los países subdesarrollados o en vías de desarrollo para embarcarse en una senda de crecimiento estable mediante técnicas de ahorro y la inversión.

En la economía de Robinson Crusoe, hay solamente un individuo – Robinson Crusoe él mismo. Actúa tanto como un productor para maximizar las ganancias, así como al consumidor para maximizar su utilidad. La posibilidad de comercio puede introducirse mediante la adición de otra persona a la economía. Esta persona es amigo de Crusoe, Viernes. Aunque en la novela juega el papel de sirvienta de Crusoe, en la economía de Robinson Crusoe que es considerado como otro actor con habilidades haciendo igual decisión como Crusoe. Junto con esto, las condiciones de Eficiencia de Pareto pueden ser analizados por traer en el concepto de la Caja de Edgeworth.

Los supuestos básicos de la economía de Robinson Crusoe son como sigue:

1. La isla está cortada del resto del mundo (y por lo tanto, no puede cambiar)
2. Hay sólo un único agente económico (Crusoe sí mismo)
3. Todos los productos básicos en la isla tienen que ser producidas o encontradas de existencias

Marco

Figura 1: Preferencia de ocio de ingresos en una economía de Robinson Crusoe.

Robinson Crusoe se asume para ser náufragos en una isla desierta. Similar a las opciones que enfrentan los hogares (proveedores de mano de obra), Crusoe tiene sólo dos actividades para participar en – ingresos o pasar su tiempo de ocio.

Los ingresos que genera la actividad en este caso está reuniendo los cocos. Como siempre, cuanto más tiempo que se pasa en el ocio, la menor cantidad de alimentos que tiene que comer y por el contrario, cuanto más tiempo pasa reunión cocos, menor es el tiempo que tiene para el ocio. Esto se muestra en la figura 1.

Función de producción y las curvas de indiferencia

Crusoe curvas de indiferencia muestran sus preferencias para el ocio y los cocos mientras el función de producción representa el tecnológico relación entre cuánto trabaja y cuantos cocos que recoge. Si los ejes que representan ocio y colección de coco son invertidos y conspiró con el mapa de indiferencia de Crusoe y función de producción, la figura 2 se puede establecer:

Figura 2: Función de producción de la economía de Robinson Crusoe y las curvas de indiferencia

La función de producción es cóncavo en dos dimensiones y cuasi-convexo en tres dimensiones. Esto significa que el Robinson ya funciona, los cocos más será capaz de reunir. Pero debido a la disminución marginal vuelve del trabajo, el número adicional de cocos que recibe de cada hora adicional de trabajo está declinando.

El punto en el cual Crusoe llegará a un equilibrio entre el número de horas que trabaja y se relaja puede ser descubierto cuando la curva de indiferencia más alta es tangente a la función de producción. Esto será punto preferido de Crusoe siempre y cuando la restricción de la tecnología se da y no puede cambiarse. En este punto de equilibrio, la pendiente de la curva de indiferencia más alta debe ser igual a la pendiente de la función de producción.

Recordemos que el Tasa marginal de sustitución es la velocidad a la que un consumidor está dispuesto a dar una buena a cambio de otra buena manteniendo el mismo nivel de utilidad. Adicionalmente, el producto marginal del insumo es más salida que puede ser producido mediante el uso de una unidad más de la entrada, suponiendo que cambian las cantidades de ningún otros insumos para la producción. Entonces,

MP_L = LA SRA._{Ocio, cocos}

donde,

MP_L = Producto marginal del trabajo, y

NR0_{Ocio, cocos} = Tasa marginal de sustitución entre el ocio y los cocos

Rol multifacético de Robinson Crusoe

Supongamos que Crusoe decide dejar de ser un productor y el consumidor al mismo tiempo. Él decide que producirá un día y consumir el siguiente. Sus dos roles de consumidores y los productores están siendo dividido y estudiaron por separado para entender la forma elemental de la teoría del consumidor y productor teoría de Microeconomía. Para dividir su tiempo entre ser un consumidor y productor, debe configurar dos colectivamente exhaustiva los mercados, el mercado de coco y el mercado laboral. También se instala una firma, de los cuales se convierte en la planta del pie accionista. La empresa quiere maximizar los beneficios por decidir cuánto trabajo a contratar y cuántos cocos para producir según sus precios. Como un trabajador de la empresa, Crusoe recogerá los salarios, como accionista, recogerá las ganancias y como consumidor, él decidirá cuánto de la firma de salida a comprar de acuerdo a sus ingresos y los precios de mercado vigentes. Supongamos que se ha creado una moneda llamada "Dólares" por Robinson para manejar sus finanzas. Para simplicidad, se asume Precio_Cocos = $1.00. Esta suposición se hace para hacer los cálculos en el ejemplo numérico fácil porque la inclusión de los precios no alterará el resultado del análisis. Para más detalles, consulte Numéraire materias primas.

Productor

Artículo principal: Teoría de la producción

Figura 3: Beneficio maximizar la condición para la firma en la economía de Robinson Crusoe

Suponer que cuando la empresa produce C cantidad de cocos totales, 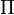$\Pi$ representa el nivel de sus ganancias. También asume cuando la tasa de salario en el cual la firma emplea mano de obra es wSe emplearán L monto del trabajo. Entonces,

$\Pi=C - wL \,$

$C=\Pi + wL \,$

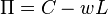
La función anterior describe las líneas iso-beneficio (el lugar geométrico de combinaciones entre el trabajo y cocos que producen una ganancia constante de Π). Las ganancias pueden incrementarse cuando el producto marginal del trabajo es igual a la tasa salarial (costo marginal de producción). Simbólicamente,

MP_L = w

Gráficamente, la línea iso de lucro debe ser tangente a la función de producción.

El intercepto vertical de la línea iso-ganancia mide el nivel de ganancia que hará firma de Robinson Crusoe. Este nivel de ganancias, Π, tiene la capacidad de compra Π dólares de los cocos. Desde Precio_Cocos es $1.00, puede adquirirse número Π de cocos. Además, la empresa se va a declarar una dividendo de dólares Π. Esto le dará al único accionista de la firma, Crusoe él mismo.

Consumidor

Artículo principal: Elección del consumidor

Figura 4: maximización problema de Robinson Crusoe mostrando su curva de línea y la indiferencia de presupuesto

Como consumidor, Crusoe tendrá que decidir cuánto trabajo (o disfrutar de ocio) y por lo tanto, consumir. Puede elegir no funciona en absoluto, ya que tiene una dotación de dólares Π de ser un accionista. En su lugar consideremos el caso más realista de lo decidido trabajar por unas horas. Su elección de consumo del trabajo puede ser ilustrado en la figura 4:

Tenga en cuenta que el trabajo se asume que es un 'mal', es decir, una mercancía que un consumidor no le gusta. Su presencia en su canasta de consumo disminuye la utilidad que se deriva. Por otro lado, los cocos son mercancías. Por esta razón las curvas de indiferencia son positivamente inclinadas. La cantidad máxima de trabajo es indicada por L'. La distancia de L' a los elegidos suministro de mano de obra (L *) da demanda de Crusoe para el ocio.

Observe la línea presupuestaria de Crusoe. Tiene una pendiente de w y pasa por el punto (0, Π). Este punto es su nivel de dotación, es decir, incluso cuando él provee 0 cantidad de mano de obra, tiene cantidad Π de los Cocos (dólares) para consumir. Teniendo en cuenta la tasa salarial, Crusoe elegirá dónde cuánto trabajar y cuánto a consumir en ese momento,

SRA._{Ocio, cocos} = w

Equilibrio

Figura 5: Equilibrio en la producción y consumo en la economía de Robinson Crusoe

En el equilibrio, la demanda de los cocos será igual a la oferta de los cocos y la demanda de trabajo será igual a la oferta de mano de obra.

Gráficamente esto se produce cuando se superponen los diagramas debajo del consumidor y productor. Observe que,

SRA._{Ocio, cocos} = w

MP_L = w

-=> NR0_{Ocio, cocos} = MP_L

Esto asegura que las pendientes de las curvas de indiferencia y la producción establecido son los mismos.

Como resultado, Crusoe termina consumiendo en el mismo punto que habría pasado si él hizo todas las decisiones anteriores juntos. En otras palabras, usando el sistema de mercado tiene el mismo resultado como elegir los planes de minimización de costo y maximización de utilidad individual. Este es un resultado importante cuando está puesto en una perspectiva de nivel macro porque implica que existe un conjunto de precios para las entradas y salidas en la economía que da como resultado el comportamiento maximización de ganancias de las empresas junto con las acciones de maximización de utilidad de los individuos en la demanda de cada bien igualando la oferta en todos los mercados. Esto significa que puede existir un equilibrio competitivo. El mérito de un equilibrio competitivo es una asignación eficiente de los recursos alcanzable. En otras palabras, ningún agente económico puede hacerse mejor sin empeorar de agente económico otro.

Posibilidades de producción con dos mercancías

Artículo principal: Frontera de posibilidades de producción

Supongamos que hay otra mercancía que Crusoe puede producir aparte de los cocos, por ejemplo, peces. Ahora, Robinson tiene que decidir cuánto tiempo de sobra para ambas actividades, es decir, cuántos cocos para reunir y cuántos peces para cazar. El lugar geométrico de las combinaciones diferentes de peces y los cocos que puede producir de dedicar diferentes cantidades de tiempo a cada actividad se conoce como el conjunto de posibilidades de producción. Esto se muestra en la figura 6:

Figura 6: Producción posibilidades ubicado en la economía de Robinson Crusoe con dos productos básicos.

El límite de la serie de posibilidades de producción es conocido como la frontera de posibilidades de producción (FPP). Esta curva mide las salidas viables que Crusoe puede producir, con una restricción tecnológica fija y dada la cantidad de recursos. En este caso, los recursos y las limitaciones tecnológicas son el trabajo de Robinson Crusoe.

Es fundamental tener en cuenta que la forma de la FFF depende de la naturaleza de la tecnología en uso. Aquí, la tecnología se refiere al tipo de rendimientos a escala frecuente. En la figura 6, la suposición subyacente es el habitual vuelve decreciente a escala, debido a que el PPF es cóncava hacia el origen. En caso de que asumimos rendimientos crecientes a escala, decir si Crusoe se embarcó en un movimiento de la producción en masa y por lo tanto ante disminuyendo los costos, el PPF sería convexa hacia el origen. El PPF es lineal con una cuesta hacia abajo en dos circunstancias:

1. Si la tecnología para recoger los cocos y caza peces exhibe constantes retornos a escala
2. Si hay sólo una entrada en producción

Así que en la economía de Robinson Crusoe, el PPF será lineal debido a la presencia de sólo una entrada.

Tasa marginal de transformación

Artículo principal: Tasa marginal de transformación

Supongamos que Crusoe puede producir 4 libras de pescado o 8 libras de cocos por hora. Si dedica L_f horas para recoger peces y L_c horas de recogida de los cocos, él producirá 4L_f libras de pescado y 8L_c libras de cocos. Supongamos que decide trabajar 12 horas al día. A continuación, el conjunto de posibilidades de producción estará formado por todas las combinaciones de pescado, F y los cocos, C, tal que

$F=4L_f \,$

$C=8L_c \,$

$L_f + L_c=12 \,$

Resolver las dos primeras ecuaciones y sustituye en el tercero, a

$F/4 + C/8=12 \,$

Esta ecuación representa de Crusoe PPF. La pendiente de este PPF mide la Tasa marginal de transformación (MRT), es decir, cuánto de la primera buena debe ser dado para arriba con el fin de aumentar la producción del segundo bien por una unidad. Si Crusoe funciona una hora menos en peces de caza, tendrá 4 menos pescado. Si dedica a esta hora extra para recoger los cocos, tendrá 8 cocos extras. El MRT es por lo tanto,

MRT _{Los cocos, pescado} $={\Delta C \over{\Delta F}} \,$ $= -8/4=-2 \,$

Ventaja comparativa

Artículo principal: Ventaja comparativa

Bajo esta sección, se introduce la posibilidad del comercio mediante la adición de otra persona a la economía. Suponga que el trabajador nuevo que se agrega a la economía de Robinson Crusoe tiene diferentes habilidades en la recopilación de los cocos y cazar peces. La segunda persona se llama "El viernes".

El viernes pueden producir 8 libras de pescado o 4 libras de cocos por hora. Si él también decide trabajar durante 12 horas, su conjunto de posibilidades de producción será determinado por las siguientes relaciones:

$F=8L_f \,$

$C=4L_c \,$

$L_f + L_c=12 \,$

$=>F/8 + C/4=12 \,$

Por lo tanto, MRT _{Los cocos, pescado} $={\Delta C \over{\Delta F}} \,$ $= -4/8=-1/2 \,$

Esto significa que por cada kilo de cocos que el viernes da para arriba, él puede producir más un kilo de pescado.

Entonces, podemos decir que el viernes tiene una ventaja comparativa en peces de caza mientras Crusoe tiene una ventaja comparativa en la recopilación de los cocos. Sus respectivos mecanismos pueden ser demostrados en el diagrama siguiente:

Figura 7: Conjunto de posibilidades de producción en la economía de Robinson Crusoe.

La producción conjunta posibilidades fijadas en la extrema derecha indica la cantidad total de ambas materias que pueden ser producidos por Crusoe y el viernes juntos. Combina lo mejor de ambos trabajadores. Si ambos trabajan para recoger los cocos solamente, la economía tendrá 144 cocos en total, 96 de Crusoe y 48 desde el viernes. (Esto puede obtenerse estableciendo F = 0 en sus respectivas ecuaciones PPF y resumirlos). Aquí la pendiente de la PPF conjunta es -1/2.

Si queremos más peces, debamos usar a esa persona que tiene una ventaja comparativa en la caza de peces (es decir, viernes) de coco reuniendo y en la caza de peces. Al viernes es producir 96 kilos de pescado, está completamente ocupado. Si la producción va a incrementarse más allá de este punto, Crusoe tendrá que empezar a peces de caza. Aquí, la pendiente de la PPF conjunta es -2. Si queremos producir sólo pescado, entonces la economía tendrá 144 kilos de pescado, 48 de Crusoe y 96 del viernes. Por lo tanto el PPF conjunta está torcida porque Crusoe y el viernes tienen ventajas comparativas en diferentes materias. Conforme la economía vuelve cada vez más maneras de producir salida y diferentes ventajas comparativas, la FFF se convierte en cóncavo.

Eficiencia de Pareto

Artículo principal: Eficiencia de Pareto

Asumir que hay c unidades de coco y f unidades de pescado disponible para el consumo en la economía de Crusoe viernes. Dado este paquete de dotación (c, f), el Pareto eficiente paquete puede determinarse en la tangencia mutua de la indiferencia de Crusoe y el viernes curvas en el Caja de Edgeworth a lo largo del Pareto establecido ()Curva de contrato). Estos son los paquetes en que Crusoe y el viernes Tasa marginal de sustitución son iguales. En una economía de intercambio simple, la curva de contrato describe el conjunto de paquetes que agotar los beneficios del comercio. Pero en una economía de Robinson Crusoe y viernes, no hay otra manera de intercambiar mercancías – para producir menos de una buena y más de la otra.

Figura 8: Producción posibilidades ubicado en economía de Robinson Crusoe y la caja de Edgeworth mostrando una situación Pareto eficiente

En la figura 8, es evidente que no puede ser una economía funcionando en una posición donde la señora de Crusoe o el viernes no es igual al MRT entre cocos y los peces Pareto eficiente. Esto es porque la tasa en la cual, dice viernes está dispuesto a comercio cocos para pescado es diferente de la tasa a la cuales los cocos pueden ser transformados en peces. Por lo tanto, hay una manera de hacer mejor el viernes por reorganizar el patrón de producción.

Por lo tanto para la eficiencia de Pareto,

MRT _{Los cocos, pescado} = SRA._{Los cocos, pescado}

(para Crusoe y el viernes)

Esto puede lograrse en un mercado competitivo por la descentralización de las decisiones de producción y consumo, es decir Crusoe y el viernes ambos resolverá sus problemas de cuánto consumir y producir de forma independiente.

Véase también

• Interpretación económica de Robinson Crusoe
• Autarquía
• Eficiencia entre producción y consumo
• Teoremas fundamentales de la economía del bienestar

Enlaces externos

Cursos de la Universidad

• Curso de Jeffrey Miron en Harvard
• Curso de Daniel McFadden en Harvard
• Curso de Yossi Spiegel en la Universidad de Tel Aviv
• Curso de Thomas M. Steger en el centro de investigación económica
• Curso de Joseph Tao-yi Wang en Walden University
• Curso de Larry Blume en el Instituto de Santa Fe
• Curso de Teng Wah Leo en la Universidad San Francisco Xavier

Artículos

• Estímulo trabaja en la capacidad de absorción
• La desafortunada inutilidad de mayoría 'estado del Arte' académico economía monetaria

Otras Páginas

• Ostanes
• Biorretroalimentacion
• J. G. Jolly
• Karuhanga Tabaro y asociados
• Tecnologia educativa
• Plantilla: embriologia del sistema endocrino
• Steve Soliz
• Arbiskov celular