Precio Superhedging
El precio superhedging es un medida de riesgo coherente. El precio de la superhedging de un cartera (A) es equivalente a la cantidad mínima necesaria para ser pagado por un cartera admisible (B) en el momento actual para que en algún tiempo futuro especificado el valor de B es al menos tan grande como A. En un mercado completo el precio superhedging es equivalente al precio de cobertura la cartera inicial.[1]
Contenido
- 1 Definición matemática
- 2 Conjunto de aceptación
- 3 Precio subhedging
- 4 Dinámica superhedging precio
- 5 Referencias
Definición matemática
Si el conjunto de medidas equivalentes martingala se denota por EMM entonces el precio de la superhedging de una cartera X es 
donde 
se define por
-
![\rho(X) = \sup_{Q \in \mathrm{EMM}} \mathbb{E}^Q[-X]](//upload.wikimedia.org/math/c/f/e/cfee442af0165640f8440640e5902b41.png)
.
![\rho(X) = \sup_{Q \in \mathrm{EMM}} \mathbb{E}^Q[-X]](http://upload.wikimedia.org/math/c/f/e/cfee442af0165640f8440640e5902b41.png)
.
definido como el anterior es una medida de riesgo coherente.[2]
Conjunto de aceptación
El conjunto de aceptación de la superhedging el precio es el negativo del conjunto de los valores de un cartera de autofinanciación en el momento terminal. Es decir
-
.
[citación necesitada]
.
[Precio subhedging
El precio subhedging es el mayor valor que puede ser pagado para que en cualquier situación posible en el tiempo futuro especificado tiene una segunda cartera vale menos o igual a la inicial. Matemáticamente se puede escribir como ![\inf_{Q \in \mathrm{EMM}} \mathbb{E}^Q[X]](http://upload.wikimedia.org/math/6/3/5/635565e210d210dadf37b3434aa00cd8.png)
. Es obvio para ver que se trata de la negativa del precio superhedging de la negativa de la reclamación inicial (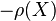
). En un mercado completo entonces el Supremum y infimum son iguales entre sí y existe un precio único de cobertura.[3] Los límites superiores e inferiores, creados por los precios de subhedging y superhedging respectivamente son la límites de no-arbitraje, un ejemplo de límites de buen-trato.[4][5]
Dinámica superhedging precio
El precio de superhedging dinámico medidas de riesgo condicional de la forma:
![\rho_t(X) = \operatorname*{ess\sup}_{Q \in EMM} \mathbb{E}^Q[-X | \mathcal{F}_t].](http://upload.wikimedia.org/math/0/c/b/0cbdc8dc7fa5917856c36f6b904cc3c1.png)
Es un resultado ampliamente demostrado que esto es constante de tiempo.[6]
Referencias
- ^ "Replicación dinámica" (pdf). p. 3. 22 de julio de 2010.
- ^ Follmer, Hans; Schied, Alexander (08 de octubre de 2008). "Medidas de riesgo coherentes y convexo" (pdf). 22 de julio de 2010.
- ^ Guo Lei (Nick) (23 de agosto de 2006). "Precios y cobertura en los mercados incompletos" (pdf). págs. 10 – 17.
- ^ John R. Birge (2008). Ingeniería financiera. Elsevier. págs. 521-524. ISBN978-0-444-51781-4.
- ^ Arai, Takuji; Fukasawa, Masaaki (2011). "Medidas de riesgo convexo para límites de buen trato" (pdf). 14 de octubre de 2011.
- ^ Penner, Irina (2007). "Medidas de riesgo dinámico convexo: tiempo de coherencia, prudencia y sostenibilidad" (pdf). 28 de agosto de 2011.